【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为边AB中点,点E、F分别在射线CA、BC上,且AE=CF,连结EF.
猜想:如图①,当点E、F分别在边CA和BC上时,线段DE与DF的大小关系为________.
探究:如图②,当点E、F分别在边CA、BC的延长线上时,判断线段DE与DF的大小关系,并加以证明.
应用:如图②,若DE=4,利用探究得到的结论,求△DEF的面积.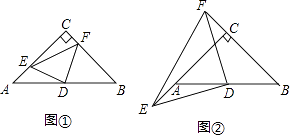
参考答案:
【答案】猜想:DE=DF.
如图1,连结CD,
∵∠ACB=90°,AC=BC,
∴∠CAD=45°,
∵D为边AB的中点,
∴CD=AD,∠BCD= ![]() ∠ACB=45°,
∠ACB=45°,
∴∠EAD=∠FCD,
在△AED和△CFD中
∴△ADE≌△CFD(SAS),
∴DE=DF,
故答案为:DE=DF;
探究:DE=DF,证明如下:
如图2,连接CD,
∵∠ACB=90°,AC=BC,
∴∠CAD=45°,
∵D为AB中点,
∴AD=CD,∠BCD= ![]() ∠ACB=45°,
∠ACB=45°,
∵∠CAD+∠EAD=∠BCD+∠FCD=180°,
∴∠EAD=∠FCD=135°,
在△ADE和△CDF中
∴△ADE≌△CDF(SAS),
∴DE=DF;
应用:
∵△ADE≌△CDF,
∴∠ADE=∠CDF,
∵∠ADC=90°,
∴∠EDF=90°,
∵DE=DF=4,
∴S△DEF= ![]() DE2=
DE2= ![]() ×42=8.
×42=8.
【解析】猜想:连接CD,可证明△ADE≌△CFD,可得出结论;探究:连接CD,同(1)可证明△ADE≌△CFD,可证得DE=DF;应用:由△ADE≌△CFD可证得∠EDF=90°,容易求得△DEF的面积.
【考点精析】本题主要考查了全等三角形的性质的相关知识点,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了预测九年级男生“排球30秒”对墙垫球的情况,从本校九年级随机抽取了n名男生进行该项目测试,并绘制出如下的频数分布直方图,其中从左到右依次分为七个组(每组含最小值,不含最大值).根据统计图提供的信息解答下列问题:
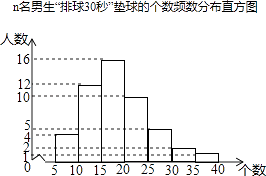
(1)求n的值.
(2)这个样本数据的中位数落在第组.
(3)若测试九年级男生“排球30秒”对墙垫球个数不低于10个为合格,根据统计结果,估计该校九年级450名男同学成绩合格的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,三条公路两两相交,交点分别为A、B、C,现计划修一个油库,要求到三条公路的距离相等,可供选择的地址有( )

A. 一处 B. 二处 C. 三处 D. 四处
-
科目: 来源: 题型:
查看答案和解析>>【题目】某通讯公司推出A、B两种手机话费套餐,这两种套餐每月都有一定的固定费用和免费通话时间,超过免费通话时间的部分收费标准为:A套餐a元/分,B套餐b元/分,使用A、B两种套餐的通话费用y(元)与通话时间x(分)之间的函数图象如图所示.
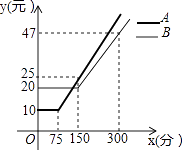
(1)当手机通话时间为50分钟时,写出A、B两种套餐的通话费用.
(2)求a,b的值.
(3)当选择B种套餐比A种套餐更合算时,求通话时间x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+mx(m>0且m≠1)与x轴交于原点O和点A,点B的坐标为(1,﹣1),连结AB,将线段AB绕点A顺时针旋转90°得到线段AC,连结OB、OC.
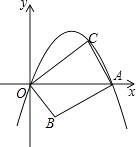
(1)求点A的横坐标.(用含m的代数式表示).
(2)若m=3,则点C的坐标为 .
(3)当点C与抛物线的顶点重合时,求四边形ABOC的面积.
(4)结合m的取值范围,直接写出∠AOC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在所给正方形网格图中完成下列各题:(用直尺画图,保留痕迹)
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点Q,使QA+QC最小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
证明:(1)CF=EB.
(2)AB=AF+2EB.

相关试题

