【题目】如图,△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,
(1)若∠A=40°,∠B=60°,求∠DCE的度数.
(2)若∠A=m,∠B=n,求∠DCE.(用m、n表示)

参考答案:
【答案】(1)10度;(2)![]()
【解析】试题分析:
(1)由已知易得∠ACB=80°,∠AEC=90°,由CD平分∠ACB可得∠ACD=40°,由∠AEC=90°、∠A=40°可得∠ACE=50°,这样就可得∠DCE=∠ACE-∠ACD=10°;
(2)把(1)中∠A=40°,∠B=60°分别换成m和n即可用含m、n的式子表达出∠DCE.
试题解析:
(1)∵△ABC中,∠A=40°,∠B=60°,
∴∠ACB=180°-40°-60°=80°,
又∵CD是∠ACB的角平分线,CE是AB边上的高,
∴∠ACD=![]() ∠ACB=40°,∠ACE=90°﹣∠A=50°,
∠ACB=40°,∠ACE=90°﹣∠A=50°,
∴∠DCE=∠ACE﹣∠ACD=50°﹣40°=10°;
(2)∵△ABC中,∠A=m,∠B=n,
∴∠ACB=180°﹣m﹣n,
又∵CD是∠ACB的角平分线,CE是AB边上的高,
∴∠ACD=![]() ∠ACB=
∠ACB=![]() ,∠ACE=90°﹣∠A=90°﹣m,
,∠ACE=90°﹣∠A=90°﹣m,
∴∠DCE=∠ACE﹣∠ACD=(90°﹣m)﹣![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+mx(m>0且m≠1)与x轴交于原点O和点A,点B的坐标为(1,﹣1),连结AB,将线段AB绕点A顺时针旋转90°得到线段AC,连结OB、OC.
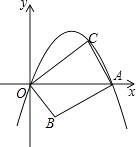
(1)求点A的横坐标.(用含m的代数式表示).
(2)若m=3,则点C的坐标为 .
(3)当点C与抛物线的顶点重合时,求四边形ABOC的面积.
(4)结合m的取值范围,直接写出∠AOC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在所给正方形网格图中完成下列各题:(用直尺画图,保留痕迹)
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点Q,使QA+QC最小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
证明:(1)CF=EB.
(2)AB=AF+2EB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点0是等边△ABC内一点,∠AOB=110°,∠BOC=α,OC=CD,
且∠DOC=60°连接OD.
(1)求证:△COD是等边三角形
(2)当α=150°时,试判断△AOD的形状,并说明理由
(3)探究:当α为多少度时,△AOD是等腰三角形

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、M在BC上,则∠EAN=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=4,点P从点C出发沿CA以每秒1个单位长度的速度向终点A运动:同时,点Q从点C出发沿CB﹣BA运动,点Q在CB上的速度为每秒2个单位长度,在BA上的速度为每秒
 个单位长度,当点P到达终点A时,点Q随之停止运动.以CP、CQ为邻边作CPMQ,设CPMQ与△ABC重叠部分图形的面积为y(平方单位),点P的运动时间为x(秒).
个单位长度,当点P到达终点A时,点Q随之停止运动.以CP、CQ为邻边作CPMQ,设CPMQ与△ABC重叠部分图形的面积为y(平方单位),点P的运动时间为x(秒).
(1)当点M落在AB上时,求x的值.
(2)当点Q在边CB上运动时,求y与x的函数关系式.
(3)在P、Q两点整个运动过程中,当CPMQ与△ABC重叠部分图形不是四边形时,求x的取值范围.
(4)以B、C、M为顶点的三角形是等腰三角形时,直接写出CP的长.
相关试题

