【题目】(1)尺规作图:如图,AB为⊙O的直径,过点A作⊙O的切线m;
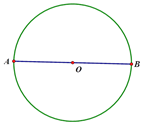
(2)在直线m上任取一点P(A点除外),连接PB交圆O与点C,请补全图形,并证明: ![]()
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】(1)过点A作AB的垂线得到⊙O的切线;
(2)连接AC,利用切线的性质得AP⊥AB,再利用圆周角定理得到∠ACB=90°,接着证明△APC~△BPA,然后利用相似三角形的性质得到结论.
(1)如图,直线m为所求作;
(2)如图,证明如下:连接AC.
∵AP是⊙O的切线,∴AP⊥AB.
又∵AB为⊙O的直径,∴∠ACB=90°,∴∠ACP=∠BAP=90°.
∵∠APC=∠BPA,∴△APC~△BPA,∴PA:PC=PB:PA,∴PA2=PCPB.
-
科目: 来源: 题型:
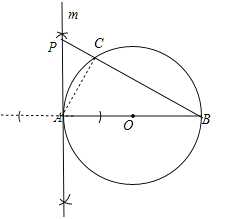
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E在BC边上,且CE︰BC=2︰3,AC与DE相交于点F,若S△EFC=8,则S△CFD=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求证:角平分线和中线重合的三角形是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请完成下面的解答过程完.如图,∠1=∠B,∠C=110°,求∠3的度数.

解:∵∠1=∠B
∴AD∥( )(内错角相等,两直线平行)
∴∠C+∠2=180°,( )
∵∠C=110°.
∴∠2=( )°.
∴∠3=∠2=70°.( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD,CD分别是△ABC两个外角的平分线.
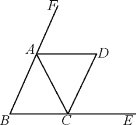
(1)求证:∠ACD=∠ADC;
(2)若∠B=60°,求证:四边形ABCD是菱形.
-
科目: 来源: 题型:
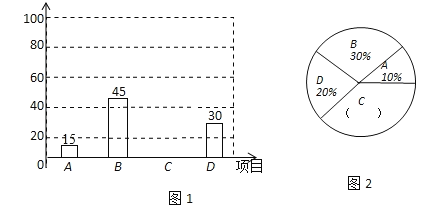
查看答案和解析>>【题目】为进一步推广“阳光体育”大课间活动,某中学对已开设的A实心球,B立定跳远,C跑步,D跳绳四种活动项目的学生喜欢情况,进行调查,随机抽取了部分学生,并将调查结果绘制成图1、图2的统计图,请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整;
(3)在扇形统计图,请计算本项调查中喜欢“跑步”部分所对应的圆心角的度数;
(4)如果全校共1200名同学,请你估算喜欢“跑步”的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
相关试题

