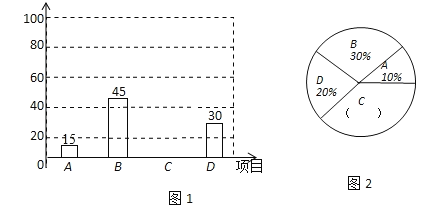
【题目】为进一步推广“阳光体育”大课间活动,某中学对已开设的A实心球,B立定跳远,C跑步,D跳绳四种活动项目的学生喜欢情况,进行调查,随机抽取了部分学生,并将调查结果绘制成图1、图2的统计图,请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整;
(3)在扇形统计图,请计算本项调查中喜欢“跑步”部分所对应的圆心角的度数;
(4)如果全校共1200名同学,请你估算喜欢“跑步”的学生人数.
参考答案:
【答案】(1)150名;(2)答案见解析;(3)144°;(4)480名
【解析】
(1)根据喜欢A项目的人数是15,所占的百分比是10%即可求得调查的总人数;
(2)利用总人数减去其它项的人数即可求得喜欢“跑步”的学生人数,然后根据百分比的意义求得百分比;
(3)利用360°乘以对应的百分比即可求解;
(4)利用总人数乘以对应的百分比即可.
(1)共调查了15÷10%=150名学生;
(2)本项调查中喜欢“跑步”的学生人数是;150﹣15﹣45﹣30=60(人),
所占百分比是:![]() 100%=40%,
100%=40%,
 ;
;
(3)“跑步”部分所对应的圆心角的度数是:360°×40%=144°;
(4)全校喜欢“跑步”的学生人数约是:1200×40%=480.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请完成下面的解答过程完.如图,∠1=∠B,∠C=110°,求∠3的度数.

解:∵∠1=∠B
∴AD∥( )(内错角相等,两直线平行)
∴∠C+∠2=180°,( )
∵∠C=110°.
∴∠2=( )°.
∴∠3=∠2=70°.( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)尺规作图:如图,AB为⊙O的直径,过点A作⊙O的切线m;
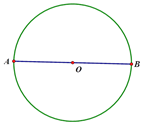
(2)在直线m上任取一点P(A点除外),连接PB交圆O与点C,请补全图形,并证明:
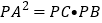
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD,CD分别是△ABC两个外角的平分线.
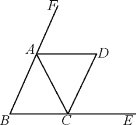
(1)求证:∠ACD=∠ADC;
(2)若∠B=60°,求证:四边形ABCD是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
-
科目: 来源: 题型:
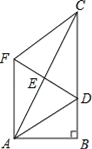
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.
求证:四边形ADCF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,长方形ABCD的边AB在y轴正半轴上,顶点A的坐标为(0,2),设顶点C的坐标为(a,b).
(1)顶点B的坐标为 ,顶点D的坐标为 (用a或b表示);
(2)如果将一个点的横坐标作为x的值,纵坐标作为y的值,代入方程2x+3y=12成立,就说这个点的坐标是方程2x+3y=12的解.已知顶点B和D的坐标都是方程2x+3y=12的解,求a,b的值;
(3)在(2)的条件下,平移长方形ABCD,使点B移动到点D,得到新的长方形EDFG,
①这次平移可以看成是先将长方形ABCD向右平移 个单位长度,再向下平移 个单位长度的两次平移;
②若点P(m,n)是对角线BD上的一点,且点P的坐标是方程2x+3y=12的解,试说明平移后点P的对应点P′的坐标也是方程2x+3y=12的解.

相关试题

