【题目】如图,平行于x轴的直线AC分别交抛物线![]() (x≥0)与
(x≥0)与![]() (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则![]() =_.
=_.

参考答案:
【答案】![]()
【解析】试题分析:设A点坐标为(0,a),利用两个函数解析式求出点B、C的坐标,然后求出AB的长度,再根据CD∥y轴,利用y1的解析式求出D点的坐标,然后利用y2求出点E的坐标,从而得到DE的长度,然后求出比值即可得解.
解:设A点坐标为(0,a),(a>0),
则x2=a,解得x=![]() ,
,
∴点B(![]() ,a),
,a),
∴AB=![]() .
.
∵![]() =a,
=a,
则x=![]() ,
,
∴点C(![]() ,a),
,a),
∵CD∥y轴,
∴点D的横坐标与点C的横坐标相同为![]() ,
,
∴y1=(![]() )2=5a,
)2=5a,
∴点D的坐标为(![]() ,5a).
,5a).
∵DE∥AC,
∴点E的纵坐标为5a,
∴![]() =5a,
=5a,
∴x=5![]() ,
,
∴点E的坐标为(5![]() ,5a),
,5a),
∴DE=5![]() -
-![]() ,
,
∴![]() =
=![]() .
.
故答案是: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式m2+m+1=0,那么代数式2018﹣2m2﹣2m的值是( )
A.2016
B.﹣2016
C.2020
D.﹣2020 -
科目: 来源: 题型:
查看答案和解析>>【题目】长为9,6,5,4的四根木条,选其中三根组成三角形,选法有( )
A.1种 B.2种 C.3种 D.4种
-
科目: 来源: 题型:
查看答案和解析>>【题目】李老师家距学校1900米,某天他步行去上班,走到路程的一半时发现忘带手机,此时离上班时间还有23分钟,于是他立刻步行回家取手机,随后骑电瓶车返回学校.已知李老师骑电瓶车到学校比他步行到学校少用20分钟,且骑电瓶车的平均速度是步行速度的5倍,李老师到家开门、取手机、启动电瓶车等共用4分钟.
(1)求李老师步行的平均速度;
(2)请你判断李老师能否按时上班,并说明理由.
-
科目: 来源: 题型:
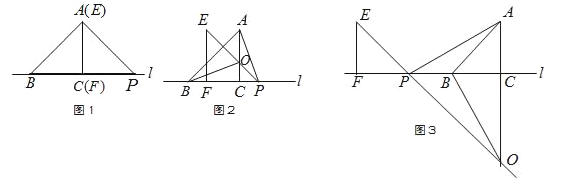
查看答案和解析>>【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)如图1,请你写出AB与AP所满足的数量关系和位置关系;
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点O,连接AP,BO.猜想并写出BO与AP所满足的数量关系和位置关系,并说明理由;
(3)将△EFP沿直线l继续向左平移到图3的位置时,EP的延长线交AC的延长线于点O,连接AP,BO.此时,BO与AP还具有(2)中的数量关系和位置关系吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=x2经过平移得到抛物线y=x2﹣2x,其对称轴与两抛物线所围成的阴影部分的面积是__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三角形的一边长为3 cm,则它的周长可能为( )
A. 4 cm B. 5 cm C. 6 cm D. 8 cm
相关试题

