Question

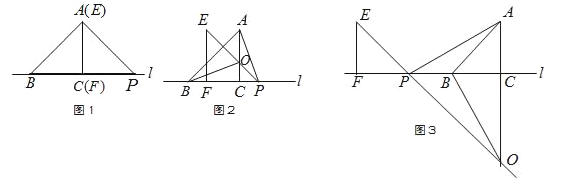
【题目】如图1，△ABC的边BC在直线l上，AC⊥BC，且AC=BC；△EFP的边FP也在直线l上，边EF与边AC重合，且EF=FP．

（1）如图1，请你写出AB与AP所满足的数量关系和位置关系；

（2）将△EFP沿直线l向左平移到图2的位置时，EP交AC于点O，连接AP，BO．猜想并写出BO与AP所满足的数量关系和位置关系，并说明理由；

（3）将△EFP沿直线l继续向左平移到图3的位置时，EP的延长线交AC的延长线于点O，连接AP，BO．此时，BO与AP还具有（2）中的数量关系和位置关系吗？请说明理由．

Answer 1

【答案】（1）AP=AB，AP⊥AB；（2）AP=BO，AP⊥BO；（3）AP=BO，AP⊥BO．

【解析】整体分析：

(1)根据△ABC与△EFP是全等的等腰直角三角形，判断△ABP是等腰直角三角形；(2)用SAS证明△ACP≌△BCO得到AP＝BO，∠CAP＝∠CBO，结合三角形的内角和可得BO⊥AP；(3)结合与理由和(2)类似.

解：(1)∵AC⊥BC，且AC＝BC，边EF与边AC重合，且EF＝FP．

∴△ABC与△EFP是全等的等腰直角三角形，

∴∠BAC＝∠CAP＝45°，AB＝AP，

∴∠BAP＝90°，

∴AP＝AB，AP⊥AB；

(2)AP＝BO，AP⊥BO．理由如下：

延长BO交AP于H点，如图2

∵∠EPF＝45°，

∴△OPC为等腰直角三角形，

∴OC＝PC，

∵在△ACP和△BCO中

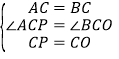
∴△ACP≌△BCO(SAS)，

∴AP＝BO，∠CAP＝∠CBO，

又∵∠AOH＝∠BOC，

∴∠AHO＝∠BCO＝90°，

∴AP⊥BO，

即BO与AP所满足的数量关系为相等，位置关系为垂直；

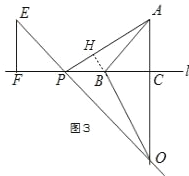
(3)BO与AP所满足AP＝BO，AP⊥BO．理由如下：

延长OB交AP于点H，如图3，

∵∠EPF＝45°，

∴∠CPO＝45°，

∴△CPO为等腰直角三角形，

∴OC＝PC，

∵在△APC和△OBC中，

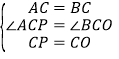
∴△APC≌△BOC(SAS)，

∴AP＝BO，∠APC＝∠COB，

而∠PBH＝∠CBO，

∴∠PHB＝∠BCO＝90°，

∴BO⊥AP，

即BO与AP所满足的数量关系为相等，位置关系为垂直．