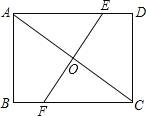
【题目】如图,在矩形纸片ABCD中,AB=6cm,BC=8cm,将矩形纸片折叠,使点C与点A重合,请在图中画出折痕,并求折痕的长.

参考答案:
【答案】图详见解析,折痕长![]() cm.
cm.
【解析】
连接AC,作出AC的垂直平分线,分别交AD、AC、BC于点E、O、F,EF即为折痕;根据勾股定理求出AC的长,根据翻折变换的性质可得AC⊥EF,OA=OC=![]() AC,再利用∠ACB的正切列式求出OF的长,再证明△AOE≌△COF,根据全等三角形对应边相等可得OE=OF,由此即可求得EF的长.
AC,再利用∠ACB的正切列式求出OF的长,再证明△AOE≌△COF,根据全等三角形对应边相等可得OE=OF,由此即可求得EF的长.
如图所示,EF即为折痕;
∵AB=6cm,BC=8cm,
∴由勾股定理可得,AC=10cm,
∵折叠后点C与点A重合,
∴AC⊥EF,OA=OC=![]() AC=
AC=![]() ×10=5cm,
×10=5cm,
∵tan∠ACB=![]() ,
,
∴![]() ,
,
解得OF=![]() cm,
cm,
∵矩形对边AD∥BC,
∴∠OAE=∠OCF,
在△AOE和△COF中,
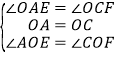 ,
,
∴△AOE≌△COF(ASA),
∴OE=OF=![]() cm,
cm,
∴折痕EF=![]() +
+![]() =
=![]() cm.
cm.
-
科目: 来源: 题型:
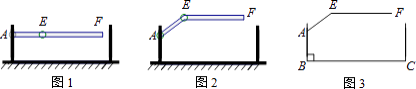
查看答案和解析>>【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x+2y=7在自然数范围内的解( )
A. 有无数对 B. 只有1对
C. 只有3对 D. 只有4对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=
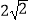 ,CD=
,CD= 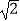 ,点P在四边形ABCD上,若P到BD的距离为
,点P在四边形ABCD上,若P到BD的距离为  ,则点P的个数为( )
,则点P的个数为( ) 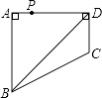
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1 , 则∠A1=;∠A1BC与∠A1CD的平分线相交于点A2 , 得∠A2;…;∠An﹣1BC与∠An﹣1CD的平分线相交于点An , 要使∠An的度数为整数,则n的值最大为 .
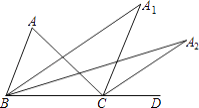
-
科目: 来源: 题型:
查看答案和解析>>【题目】按照如下步骤计算:6﹣2÷(
 +
+ 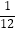 ﹣
﹣ 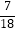 ﹣
﹣ 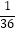 ).
).
(1)计算:( +
+ 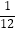 ﹣
﹣ 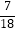 ﹣
﹣ 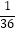 )÷6﹣2;
)÷6﹣2;
(2)根据两个算式的关系,直接写出6﹣2÷( +
+ 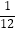 ﹣
﹣ 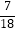 ﹣
﹣ 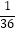 )的结果.
)的结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】某通讯器材商场,计划用40000元从厂家购进若干部新型手机,以满足市场需求. 已知该厂家生产三种不同型号的手机,出厂价分别为:甲种型号手机每部1200元,乙种型号手机每部400元,丙种型号手机每部800元.
(1)若该商场同时购进其中两种不同型号的手机共40部,并将40000元恰好用完. 请你帮助该商场研究一下进货方案;
(2)商场每销售一部甲种型号手机可获利120元,每销售一部乙种型号手机可获利80元,每销售一部丙种型号手机可获利120元,那么在同时购进两种不同型号手机的几种方案中,哪种进货方案获利最多?
相关试题

