【题目】如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD= ![]() ,CD=
,CD= ![]() ,点P在四边形ABCD上,若P到BD的距离为
,点P在四边形ABCD上,若P到BD的距离为 ![]() ,则点P的个数为( )
,则点P的个数为( ) 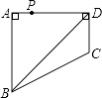
A.1
B.2
C.3
D.4
参考答案:
【答案】B
【解析】解:过点A作AE⊥BD于E,过点C作CF⊥BD于F, 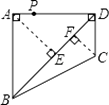
∵∠BAD=∠ADC=90°,AB=AD= ![]() ,CD=
,CD= ![]() ,
,
∴∠ABD=∠ADB=45°,
∴∠CDF=90°﹣∠ADB=45°,
∵sin∠ABD= ![]() ,
,
∴AE=ABsin∠ABD=2 ![]() sin45°
sin45°
=2 ![]()
![]() =2>
=2> ![]() ,
,
所以在AB和AD边上有符合P到BD的距离为 ![]() 的点2个,
的点2个,
∵sin∠CDF= ![]() ,
,
∴CF=CDsin∠CDF= ![]()
![]() =1<
=1< ![]() ,
,
所以在边BC和CD上没有到BD的距离为 ![]() 的点,
的点,
总之,P到BD的距离为 ![]() 的点有2个.
的点有2个.
故选:B.
【考点精析】解答此题的关键在于理解点到直线的距离的相关知识,掌握从直线外一点到这条直线的垂线段的长度叫做点到直线的距离,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,∠ACB=25°,现将ABCD沿EF折叠,使点C与点A重合,点D落在G处,则∠GFE的度数( )
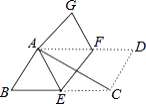
A.135°
B.120°
C.115°
D.100° -
科目: 来源: 题型:
查看答案和解析>>【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
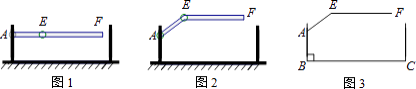
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x+2y=7在自然数范围内的解( )
A. 有无数对 B. 只有1对
C. 只有3对 D. 只有4对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=6cm,BC=8cm,将矩形纸片折叠,使点C与点A重合,请在图中画出折痕,并求折痕的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1 , 则∠A1=;∠A1BC与∠A1CD的平分线相交于点A2 , 得∠A2;…;∠An﹣1BC与∠An﹣1CD的平分线相交于点An , 要使∠An的度数为整数,则n的值最大为 .
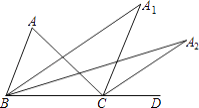
-
科目: 来源: 题型:
查看答案和解析>>【题目】按照如下步骤计算:6﹣2÷(
 +
+ 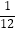 ﹣
﹣ 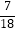 ﹣
﹣ 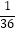 ).
).
(1)计算:( +
+ 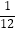 ﹣
﹣ 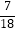 ﹣
﹣ 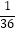 )÷6﹣2;
)÷6﹣2;
(2)根据两个算式的关系,直接写出6﹣2÷( +
+ 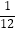 ﹣
﹣ 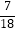 ﹣
﹣ 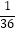 )的结果.
)的结果.
相关试题

