【题目】如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1 , 则∠A1=;∠A1BC与∠A1CD的平分线相交于点A2 , 得∠A2;…;∠An﹣1BC与∠An﹣1CD的平分线相交于点An , 要使∠An的度数为整数,则n的值最大为 . 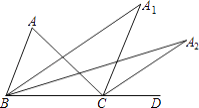
参考答案:
【答案】32°;6
【解析】解:由三角形的外角性质得,∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC, ∵∠ABC的平分线与∠ACD的平分线交于点A1 ,
∴∠A1BC= ![]() ∠ABC,∠A1CD=
∠ABC,∠A1CD= ![]() ∠ACD,
∠ACD,
∴∠A1+∠A1BC= ![]() (∠A+∠ABC)=
(∠A+∠ABC)= ![]() ∠A+∠A1BC,
∠A+∠A1BC,
∴∠A1= ![]() ∠A=
∠A= ![]() 64°=32°;
64°=32°;
∵A1B、A1C分别平分∠ABC和∠ACD,
∴∠ACD=2∠A1CD,∠ABC=2∠A1BC,
而∠A1CD=∠A1+∠A1BC,∠ACD=∠ABC+∠A,
∴∠A=2∠A1 ,
∴∠A1= ![]() ∠A,
∠A,
同理可得∠A1=2∠A2 ,
∴∠A2= ![]() ∠A,
∠A,
∴∠A=2n∠An ,
∴∠An=( ![]() )n∠A=
)n∠A= ![]() ,
,
∵∠An的度数为整数,
∵n=6.
故答案为:32°,6.
根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,根据角平分线的定义可得∠A1BC= ![]() ∠ABC,∠A1CD=
∠ABC,∠A1CD= ![]() ∠ACD,然后整理得到∠A1=
∠ACD,然后整理得到∠A1= ![]() ∠A,由∠A1CD=∠A1+∠A1BC,∠ACD=∠ABC+∠A,而A1B、A1C分别平分∠ABC和∠ACD,得到∠ACD=2∠A1CD,∠ABC=2∠A1BC,于是有∠A=2∠A1 , 同理可得∠A1=2∠A2 , 即∠A=22∠A2 , 因此找出规律.
∠A,由∠A1CD=∠A1+∠A1BC,∠ACD=∠ABC+∠A,而A1B、A1C分别平分∠ABC和∠ACD,得到∠ACD=2∠A1CD,∠ABC=2∠A1BC,于是有∠A=2∠A1 , 同理可得∠A1=2∠A2 , 即∠A=22∠A2 , 因此找出规律.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x+2y=7在自然数范围内的解( )
A. 有无数对 B. 只有1对
C. 只有3对 D. 只有4对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=
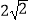 ,CD=
,CD= 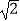 ,点P在四边形ABCD上,若P到BD的距离为
,点P在四边形ABCD上,若P到BD的距离为  ,则点P的个数为( )
,则点P的个数为( ) 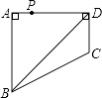
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=6cm,BC=8cm,将矩形纸片折叠,使点C与点A重合,请在图中画出折痕,并求折痕的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】按照如下步骤计算:6﹣2÷(
 +
+ 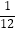 ﹣
﹣ 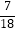 ﹣
﹣ 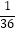 ).
).
(1)计算:( +
+ 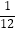 ﹣
﹣ 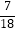 ﹣
﹣ 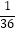 )÷6﹣2;
)÷6﹣2;
(2)根据两个算式的关系,直接写出6﹣2÷( +
+ 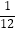 ﹣
﹣ 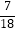 ﹣
﹣ 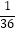 )的结果.
)的结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】某通讯器材商场,计划用40000元从厂家购进若干部新型手机,以满足市场需求. 已知该厂家生产三种不同型号的手机,出厂价分别为:甲种型号手机每部1200元,乙种型号手机每部400元,丙种型号手机每部800元.
(1)若该商场同时购进其中两种不同型号的手机共40部,并将40000元恰好用完. 请你帮助该商场研究一下进货方案;
(2)商场每销售一部甲种型号手机可获利120元,每销售一部乙种型号手机可获利80元,每销售一部丙种型号手机可获利120元,那么在同时购进两种不同型号手机的几种方案中,哪种进货方案获利最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大树AB与大数CD相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为1m/s,小华行走到点E的时间是( )

A. 13s B. 8s C. 6s D. 5s
相关试题

