【题目】猜想与证明: 如图,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM,EM.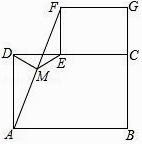
(1)试猜想写出DM与EM的数量关系,并证明你的结论. 拓展与延伸:
(2)若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则(1)中的结论是否仍然成立?请直接写出你的判断.
参考答案:
【答案】
(1)解:结论:DM=EM.
理由:如图1,延长EM交AD于点H,
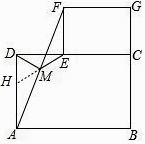
∵四边形ABCD和ECGF是矩形,
∴AD//EF,
∴∠EFM=∠HAM,
又∵∠FME=∠AMH,FM=AM,
在△FME和△AMH中,
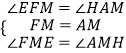 ,
,
∴△FME≌△AMH,
∴HM=EM,
在直角△HDE中,HM=EM,
∴DM=HM=EM,
∴DM=EM.
(2)解:成立.(证明方法类似)
【解析】(1)结论:DM=EM.只要证明△FME≌△AMH,推出HM=EM,在直角△HDE中利用斜边中线的性质即可证明.(2)结论不变.证明方法类似.
【考点精析】利用矩形的性质和正方形的判定方法对题目进行判断即可得到答案,需要熟知矩形的四个角都是直角,矩形的对角线相等;先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OP平分∠BOA,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论中错误的是( )

A. PC=PD B. OC=OD C. OC=OP D. ∠CPO=∠DPO
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.

(1)求证:CE是⊙O的切线;
(2)若AE=1,CE=2,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车
乙种客车
载客量(座/辆)
60
45
租金(元/辆)
550
450
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】本学期我们学习了“有理数乘方”运算,知道乘方的结果叫做“幂”,下面介绍一种有关“幂”的新运算.
定义:am 与 an(a≠0,m、n 都是正整数)叫做同底数幂,同底数幂除法记作 am÷an .
运算法则如下:am÷an=
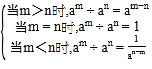
根据“同底数幂除法”的运算法则,回答下列问题:
(1)填空:
 = ,43÷45= .
= ,43÷45= .(2)如果 3x-1÷33x-4=
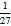 ,求出 x 的值.
,求出 x 的值.(3)如果(x﹣1)2x+2÷(x﹣1)x+6=1,请直接写出 x 的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
 x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC//x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC//x轴,点P是直线AC下方抛物线上的动点.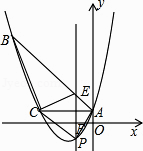
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2=_____.

相关试题

