【题目】如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2=_____.

参考答案:
【答案】45°
【解析】
如图,连接AC,BC,根据勾股定理及其逆定理,求得∠ACB=90°,∠CAB=45°.再证明四边形ADFC是平行四边形,可得AC∥DF,根据两直线平行,同位角相等可得∠2=∠DAC,在Rt△ABD中,∠1+∠DAB=90°,又因∠DAB=∠DAC+∠CAB,所以∠1+∠CAB+∠DAC=90°,即可得∠1+∠DAC=45°,即∠1+∠2=∠1+∠DAC=45°.
如图,连接AC,BC.

根据勾股定理,AC=BC=![]() ,AB=
,AB=![]() .
.
∵(![]() )2+(
)2+(![]() )2=(
)2=(![]() )2,
)2,
∴∠ACB=90°,∠CAB=45°.
∵AD∥CF,AD=CF,
∴四边形ADFC是平行四边形,
∴AC∥DF,
∴∠2=∠DAC(两直线平行,同位角相等),
在Rt△ABD中,
∠1+∠DAB=90°(直角三角形中的两个锐角互余);
又∵∠DAB=∠DAC+∠CAB,
∴∠1+∠CAB+∠DAC=90°,
∴∠1+∠DAC=45°,
∴∠1+∠2=∠1+∠DAC=45°.
故答案为:45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】猜想与证明: 如图,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM,EM.
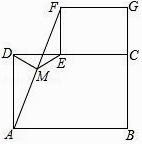
(1)试猜想写出DM与EM的数量关系,并证明你的结论. 拓展与延伸:
(2)若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则(1)中的结论是否仍然成立?请直接写出你的判断. -
科目: 来源: 题型:
查看答案和解析>>【题目】本学期我们学习了“有理数乘方”运算,知道乘方的结果叫做“幂”,下面介绍一种有关“幂”的新运算.
定义:am 与 an(a≠0,m、n 都是正整数)叫做同底数幂,同底数幂除法记作 am÷an .
运算法则如下:am÷an=
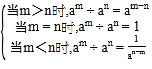
根据“同底数幂除法”的运算法则,回答下列问题:
(1)填空:
 = ,43÷45= .
= ,43÷45= .(2)如果 3x-1÷33x-4=
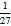 ,求出 x 的值.
,求出 x 的值.(3)如果(x﹣1)2x+2÷(x﹣1)x+6=1,请直接写出 x 的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
 x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC//x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC//x轴,点P是直线AC下方抛物线上的动点.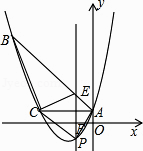
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠A和∠B互补,且∠A>∠B,给出下列四个式子:①90°﹣∠B;②∠A﹣90°;③
 (∠A+∠B)④
(∠A+∠B)④ (∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号)
(∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】“囧”(jiǒng)是一个风靡网络的流行词,像一个人脸郁闷的神情.如图所示,一张边长为8cm的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为xcm、ycm,剪去的两个小直角三角形的两直角边长也分别为xcm、ycm.

(1)用含有x、y的代数式表示图中“囧”(阴影部分)的面积.
(2)当x=8,y=2时,求此时“囧”(阴影部分)的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段MN=3cm,在线段MN上取一点P,使PM=PN;延长线段MN到点A,使AN=
 MN;延长线段NM到点B,使BN=3BM.
MN;延长线段NM到点B,使BN=3BM.(1)根据题意,画出图形;
(2)求线段AB的长;
(3)试说明点P是哪些线段的中点.
相关试题

