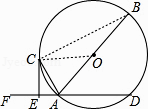
【题目】如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E. 
(1)求证:CE是⊙O的切线;
(2)若AE=1,CE=2,求⊙O的半径.
参考答案:
【答案】
(1)证明:连接CO,

∵OA=OC,
∴∠OCA=∠OAC,
∵AC平分∠FAB,
∴∠OCA=∠CAE,
∴OC//FD,
∵CE⊥DF,
∴OC⊥CE,
∴CE是⊙O的切线;
(2)证明:连接BC,
在Rt△ACE中,AC= ![]() =
= ![]() =
= ![]() ,
,
∵AB是⊙O的直径,
∴∠BCA=90°,
∴∠BCA=∠CEA,
∵∠CAE=∠CAB,
∴△ABC∽△ACE,
∴ ![]() =
= ![]() ,
,
∴ ![]() ,
,
∴AB=5,
∴AO=2.5,即⊙O的半径为2.5.
【解析】(1)证明:连接CO,证得∠OCA=∠CAE,由平行线的判定得到OC//FD,再证得OC⊥CE,即可证得结论;(2)证明:连接BC,由圆周角定理得到∠BCA=90°,再证得△ABC∽△ACE,根据相似三角形的性质即可证得结论.
【考点精析】本题主要考查了角平分线的性质定理和切线的判定定理的相关知识点,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.

(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是 ;
(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,直接写出x的值;若不存在,请说明理由.
(4)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+
 )海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
)海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OP平分∠BOA,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论中错误的是( )

A. PC=PD B. OC=OD C. OC=OP D. ∠CPO=∠DPO
-
科目: 来源: 题型:
查看答案和解析>>【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车
乙种客车
载客量(座/辆)
60
45
租金(元/辆)
550
450
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】猜想与证明: 如图,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM,EM.
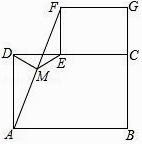
(1)试猜想写出DM与EM的数量关系,并证明你的结论. 拓展与延伸:
(2)若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则(1)中的结论是否仍然成立?请直接写出你的判断. -
科目: 来源: 题型:
查看答案和解析>>【题目】本学期我们学习了“有理数乘方”运算,知道乘方的结果叫做“幂”,下面介绍一种有关“幂”的新运算.
定义:am 与 an(a≠0,m、n 都是正整数)叫做同底数幂,同底数幂除法记作 am÷an .
运算法则如下:am÷an=
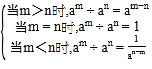
根据“同底数幂除法”的运算法则,回答下列问题:
(1)填空:
 = ,43÷45= .
= ,43÷45= .(2)如果 3x-1÷33x-4=
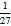 ,求出 x 的值.
,求出 x 的值.(3)如果(x﹣1)2x+2÷(x﹣1)x+6=1,请直接写出 x 的值.
相关试题

