【题目】如图,已知直线![]() :
:![]() 与x轴交于点B,直线
与x轴交于点B,直线![]()
![]() 与y轴交于点C,且它们都经过点D(1,
与y轴交于点C,且它们都经过点D(1,![]() )
)
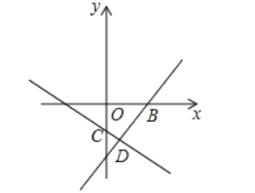

(1)求C、B两点的坐标;
(2)设点P(t,0),且t>3,如果△BDP和△CDP的面积相等,求t的值;
(3)在(2)的条件下,在第四象限内,以CP为腰作等腰直角三角形△CPQ,请直接写出点Q的坐标.
参考答案:
【答案】(1)B (3,0),C (0,2);(2)t=5;(3)Q(7,5).
【解析】
(1)根据待定系数法,可得函数解析式,根据自变量与函数值的对应关系,可得B、C点坐标;
(2)根据面积的和差,可得关于t的方程,根据解方程,可得答案;
(3)根据全等三角形的判定与性质,可得PF,PQ的长,根据点的坐标的意义,可得Q点的坐标.
(1)将(1, ![]() )代入
)代入![]() ,解得n=4,
,解得n=4,
即![]() ,当y=0时,
,当y=0时, ![]() .
.
解得x=3,
即B点坐标为(3,0);
将(1, ![]() )代入
)代入![]() ,解得m=2,
,解得m=2,
即![]() ,当x=0时,
,当x=0时, ![]() .
.
即C点坐标为(0,2);
(2)连接PC,PD,如图1,

S![]() =
=![]() (t3)×|
(t3)×|![]() |=
|=![]() (t3);
(t3);
当y=0时, ![]() ,解得x=3,即E点坐标为(3,0).
,解得x=3,即E点坐标为(3,0).
S![]() =S
=S![]() S
S![]() =
=![]() (t+3)×
(t+3)×![]()
![]() ×(t+3)×|2|=
×(t+3)×|2|=![]() (t+3)
(t+3)
由△BDP和△CDP的面积相等,得
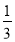 (t+3)=
(t+3)=![]() (t3).
(t3).
解得t=5.
(3)如图2,
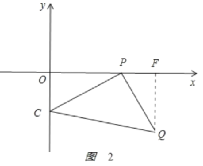
作QF⊥x轴于F点.
由△CPQ是等腰直角三角形,得
CP=PQ,∠CPQ=90°.
∠OPC+∠PCO=90°,∠OPC+∠QPF=90°,
∴∠PCO=∠QPF.
在△CPO和△PQF中,
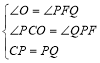 ,
,
∴△CPO≌△PQF(AAS),
∴PF=OC=2,FQ=OP=5,
Q点的横坐标为5+2=7,Q点的纵坐标为5,
即Q(7,5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD中,AB∥CD,且AB=2CD,E. F分别是AB、BC的中点,EF与BD相交于点M.

(1)求证:四边形CBED是平行四边形.
(2)若DB=9,求BM的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数
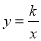 (x>0)的图象与一次函数y=3x的图象相交于点A,其横坐标为2.
(x>0)的图象与一次函数y=3x的图象相交于点A,其横坐标为2.(1)求k的值;
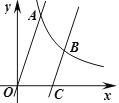
(2)点B为此反比例函数图象上一点,其纵坐标为3.过点B作CB∥OA,交x轴于点C,求点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划成立下列学生社团: A.合唱团: B.英语俱乐部: C.动漫创作社; D.文学社:E.航模工作室为了解同学们对上述学生社团的喜爱情况某课题小组在全校学生中随机抽取了部分同学,进行“你最喜爱的一个学生社团”的调查,根据调查结果绘制了如下尚不完整的统计图.
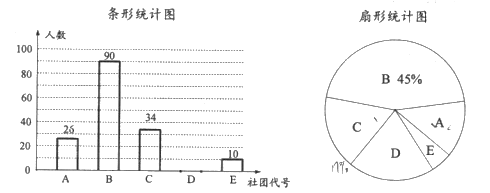
请根据以上信息,解决下列问题:
(1)本次接受调查的学生共有多少人;
(2)补全条形统计图,扇形统计图中D选项所对应扇形的圆心角为多少;
(3)若该学校共有学生3000人,估计该学校学生中喜爱合唱团和动漫创作社的总人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂生产一种夹克和T恤,夹克每件定价180元,T恤每件定价60元,厂家在开展促销活动期间,向顾客提供了两种优惠方案:①买一件夹克送一件T恤;②夹克和T恤都按定价的80%付款;现在某客户要到该厂购买夹克30件,T恤
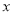 件(
件(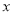 >
>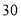 ).
).(1)若该客户按方案①购买付款 元(用含
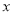 的式子表示);若该客户按方案②购买付款 元(用含
的式子表示);若该客户按方案②购买付款 元(用含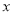 的式子表示).
的式子表示).(2)当
 时,通过计算说明方案①、方案②哪种方案购买较为合算?
时,通过计算说明方案①、方案②哪种方案购买较为合算?(3)当
 时,你能给出更为省钱的购买方案吗?试写出你的购买方法.
时,你能给出更为省钱的购买方案吗?试写出你的购买方法. -
科目: 来源: 题型:
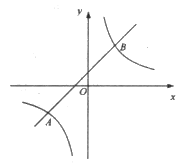
查看答案和解析>>【题目】如图,一次函数
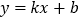 的图像与反比例函数
的图像与反比例函数 的图像交于点
的图像交于点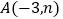 ,,
,,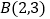
(1)求反比例函数与一次函数的函数表达式
(2)请结合图像直接写出不等式
 的解集;
的解集;(3)若点P为x轴上一点,△ABP的面积为10,求点P的坐标,
相关试题

