【题目】如图,在△ABC中,∠B=90°,AB=BC=5cm,点Q从点A开始沿AB边向点B以lcm/s的速度移动点P从点B开始沿BC边向点C以2cm/s速度移动,两点同时出发,连接PQ.
(1)经过多长时间后,△PBQ的面积等于4cm2?
(2)△PBQ的面积能否等于7cm2?试说明理由.

参考答案:
【答案】(1)1秒后,△PBQ的面积等于4cm2;(1)△PBQ的面积不能等于7cm2.
【解析】试题(1)点Q从点A开始沿AB边向点B以1cm/s的速度移动,点P从点B开始沿BC边向点C以2cm/s的速度移动,表示出BQ和BP的长度,利用三角形的面积公式可列方程求解.
(2)参照(1)的解法列出方程,根据根的判别式来判断该方程的根的情况.
试题解析:(1)设x秒后,PBQ的面积等于4cm2 ,
此时,AQ=x cm, QB=(5-x)cm. BP=2xcm,
由![]() QB·BP=4得
QB·BP=4得![]() (5-x)·2x=4 ,
(5-x)·2x=4 ,
整理,得x2-5x+4=0,
解得x1=l,x2=4(不合题意,舍去)
所以1秒后,△PBQ的面积等于4cm2 .
(2)根据题意,得![]() (5-x)·2x=7 ,
(5-x)·2x=7 ,
整理,得x2-5x+7=0 ,
因为b2-4ac=25-28<0,
所以此方程无解,即△PBQ的面积不能等于7cm2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+3与坐标轴的两个交点A、B.
(1)求抛物线的解析式; (2)画出抛物线的图象.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一批名牌衬衣,平均每天可售出20件,每件衬衣盈利40元.为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衣降价1元,商场平均每天可多售出2件.
(1)若商场平均每天盈利1200元,每件衬衣应降价多少元?
(2)若要使商场平均每天的盈利最多,每件衬衣应降价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图在直角坐标系中,点A在y轴上,BC⊥x轴于点C,点A关于直线OB的对称点D恰好在BC上,点E与点O关于直线BC对称,∠OBC=35°,则∠OED的度数为( )
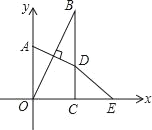
A.10°B.20°C.30°D.35°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)求C、D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足S△PCD=
 S△BCD,求点P的坐标.
S△BCD,求点P的坐标.
-
科目: 来源: 题型:
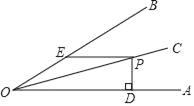
查看答案和解析>>【题目】已知OC平分∠AOB,点P为OC上一点,PD⊥OA于D,且PD=3cm,过点P作PE∥OA交OB于E,∠AOB=30°,求PE的长度_____cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),结合所给的平面直角坐标系解答下列问题:
(1)画出△ABC关于原点O对称的△A1B1C1.
(2)平移△ABC,使点A移动到点A2(0,2),画出平移后的△A2B2C2并写出点B2、C2的坐标.
(3)在△ABC、△A1B1C1、△A2B2C2中,△A2B2C2与 成中心对称,其对称中心的坐标为 .

相关试题

