【题目】如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),结合所给的平面直角坐标系解答下列问题:
(1)画出△ABC关于原点O对称的△A1B1C1.
(2)平移△ABC,使点A移动到点A2(0,2),画出平移后的△A2B2C2并写出点B2、C2的坐标.
(3)在△ABC、△A1B1C1、△A2B2C2中,△A2B2C2与 成中心对称,其对称中心的坐标为 .

参考答案:
【答案】(1)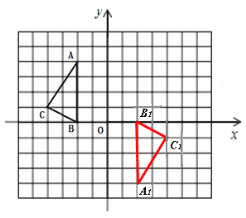 (2)平移后的△A2B2C2如图所示
(2)平移后的△A2B2C2如图所示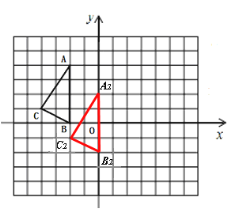 点B2、C2的坐标分别为(0,-2),(-2,-1)(3)△A1B1C1;(1,-1)
点B2、C2的坐标分别为(0,-2),(-2,-1)(3)△A1B1C1;(1,-1)
【解析】解:(1)△ABC关于原点O对称的△A1B1C1如图所示:

(2)平移后的△A2B2C2如图所示:

点B2、C2的坐标分别为(0,-2),(-2,-1)。
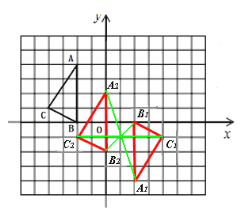
(3)△A1B1C1;(1,-1)。
(1)根据中心对称的性质,作出A、B、C三点关于原点的对称点A1、B1、C1,连接即可。
(2)根据平移的性质,点A(-2,4)→A2(0,2),横坐标加2,纵坐标减2,所以将B(-2,0)、C(-4,1)横坐标加2,纵坐标减2得到B2(0,-2)、C2(-2,-1),连接即可。
(3)如图所示。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=90°,AB=BC=5cm,点Q从点A开始沿AB边向点B以lcm/s的速度移动点P从点B开始沿BC边向点C以2cm/s速度移动,两点同时出发,连接PQ.
(1)经过多长时间后,△PBQ的面积等于4cm2?
(2)△PBQ的面积能否等于7cm2?试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)求C、D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足S△PCD=
 S△BCD,求点P的坐标.
S△BCD,求点P的坐标.
-
科目: 来源: 题型:
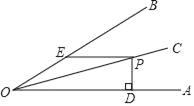
查看答案和解析>>【题目】已知OC平分∠AOB,点P为OC上一点,PD⊥OA于D,且PD=3cm,过点P作PE∥OA交OB于E,∠AOB=30°,求PE的长度_____cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,△ABC绕点C顺时针旋转一定角度得到△DEC,点D恰好落在AB边上,连接AE. 求:
(1)旋转角的度数;
(2)AE的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市某一城市美化工程招标时,有甲、乙两个工程队投标,经测算:甲队单独完成这项工程需要60天,若由甲队先做20天,剩下的工程由甲、乙合作24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成工程省钱?还是由甲乙两队全程合作完成该工程省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习完第十二章后,张老师让同学们独立完成课本56页第9题:“如图1,
 ,
, ,
, ,
, ,垂足分别为
,垂足分别为 ,
, ,
, ,
, ,求
,求 的长.”
的长.”
(1)请你也独立完成这道题:
(2)待同学们完成这道题后,张老师又出示了一道题:
在课本原题其它条件不变的前提下,将
 所在直线旋转到
所在直线旋转到 的外部(如图2),请你猜想
的外部(如图2),请你猜想 ,
, ,
, 三者之间的数量关系,直接写出结论:_______.(不需证明)
三者之间的数量关系,直接写出结论:_______.(不需证明)(3)如图3,将(1)中的条件改为:在
 中,
中, ,
, ,
, ,
, 三点在同一条直线上,并且有∠BEC=∠ADC=∠BCA=
三点在同一条直线上,并且有∠BEC=∠ADC=∠BCA= ,其中
,其中 为任意钝角,那么(2)中你的猜想是否还成立?若成立,请证明;若不成立,请说明理由:
为任意钝角,那么(2)中你的猜想是否还成立?若成立,请证明;若不成立,请说明理由:
相关试题

