【题目】已知,如图在直角坐标系中,点A在y轴上,BC⊥x轴于点C,点A关于直线OB的对称点D恰好在BC上,点E与点O关于直线BC对称,∠OBC=35°,则∠OED的度数为( )
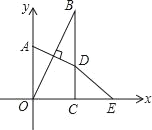
A.10°B.20°C.30°D.35°
参考答案:
【答案】B
【解析】
先根据平行线的性质求出∠AOB的度数,由直角三角形的性质得出∠BOC的度数,再根据点A关于直线OB的对称点D恰好在BC上得出OB是线段AD的垂直平分线,故可得出∠BOD的度数,进而得出∠DOC的度数,由点E与点O关于直线BC对称可知BC是OE的垂直平分线,故可得出∠DOC=∠OED.
解:连接OD,
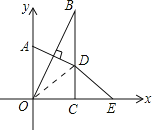
∵BC⊥x轴于点C,∠OBC=35°,
∴∠AOB=∠OBC=35°,∠BOC=90°-35°=55°.
∵点A关于直线OB的对称点D恰好在BC上,
∴OB是线段AD的垂直平分线,
∴∠BOD=∠AOB=35°,
∴∠DOC=∠BOC-∠BOD=55°-35°=20°.
∵点E与点O关于直线BC对称,
∴BC是OE的垂直平分线,
∴∠DOC=∠OED=20°.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数 y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线 x=1,下列结论:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0其中正确的是( ).

A. ①②③④ B. ①②④ C. ①③④ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+3与坐标轴的两个交点A、B.
(1)求抛物线的解析式; (2)画出抛物线的图象.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一批名牌衬衣,平均每天可售出20件,每件衬衣盈利40元.为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衣降价1元,商场平均每天可多售出2件.
(1)若商场平均每天盈利1200元,每件衬衣应降价多少元?
(2)若要使商场平均每天的盈利最多,每件衬衣应降价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=90°,AB=BC=5cm,点Q从点A开始沿AB边向点B以lcm/s的速度移动点P从点B开始沿BC边向点C以2cm/s速度移动,两点同时出发,连接PQ.
(1)经过多长时间后,△PBQ的面积等于4cm2?
(2)△PBQ的面积能否等于7cm2?试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)求C、D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足S△PCD=
 S△BCD,求点P的坐标.
S△BCD,求点P的坐标.
-
科目: 来源: 题型:
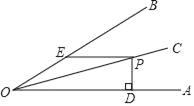
查看答案和解析>>【题目】已知OC平分∠AOB,点P为OC上一点,PD⊥OA于D,且PD=3cm,过点P作PE∥OA交OB于E,∠AOB=30°,求PE的长度_____cm.
相关试题

