【题目】某商店如果将进货价为8元的商品按每件10元售出,每天可销售200件,现在采用提高售价,减少进货量的方法增加利润,已知这种商品每涨价0.5元,其销量就减少10件.
(1)要使每天获得利润700元,请你帮忙确定售价;
(2)问售价定在多少时能使每天获得的利润最多?并求出最大利润.
参考答案:
【答案】(1)13元或15元(2)14元,最大利润为720元
【解析】
试题分析:(1)如果设每件商品提高x元,可先用x表示出单件的利润以及每天的销售量,然后根据总利润=单价利润×销售量列出关于x的方程,进而求出未知数的值.
(2)首先设应将售价提为x元时,才能使得所赚的利润最大为y元,根据题意可得:y=(x﹣8)(200﹣![]() ×10),然后化简配方,即可求得答案.
×10),然后化简配方,即可求得答案.
试题解析:(1)设每件商品提高x元,
则每件利润为(10+x﹣8)=(x+2)元,
每天销售量为(200﹣20x)件,
依题意,得:
(x+2)(200﹣20x)=700.
整理得:x2﹣8x+15=0.
解得:x1=3,x2=5.
∴把售价定为每件13元或15元能使每天利润达到700元;
答:把售价定为每件13元或15元能使每天利润达到700元.
(2)设应将售价定为x元时,才能使得所赚的利润最大为y元,
根据题意得:
y=(x﹣8)(200﹣![]() ×10),
×10),
=﹣20x2+560x﹣3200,
=﹣20(x2﹣28x)﹣3200,
=﹣20(x2﹣28x+142)﹣3200+20×142
=﹣20(x﹣14)2+720,
∴x=14时,利润最大y=720.
答:应将售价定为14元时,才能使所赚利润最大,最大利润为720元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板的两直角边所在直线分别与直线BC,CD交于点M,N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是__________________;
(2)如图2,若点O在正方形的中心(即两对角线的交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说理)

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)根据下面给出的数轴,解答下面的问题:

①请你根据图中A、B两点的位置,分别写出它们所表示的有理数A:______,B:______;
②观察数轴,与点A的距离为4的点表示的数是:______;
③若将数轴折叠,使得A点与-3表示的点重合,则B点与数______表示的点重合.
(2)如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.

①当0<t<5,用含t的式子填空:BP=______,AQ=______;
②当t=2时,求PQ的值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解
在△ABC中,AB、BC、AC三边的长分别为
 、
、 、2,求这个三角形的面积.
、2,求这个三角形的面积.解法一:如图1,因为△ABC是等腰三角形,并且底AC=2,根据勾股定理可以求得底边的高AF为1,所以S△ABC=
 ×2×1=1.
×2×1=1.解法二:建立边长为1的正方形网格,在网格中画出△ABC,使△ABC三个顶点都在小正方形的顶点处,如图2所示,借用网格面积可得S△ABC=S矩形ADEC﹣S△ABD﹣S△EBC=1.
方法迁移:请解答下面的问题:
在△ABC中,AB、AC、BC三边的长分别为
 、
、 、
、 ,求这个三角形的面积.
,求这个三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=
 ,AD=2,点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F,当BE的长为________时,△CDF为等腰三角形。
,AD=2,点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F,当BE的长为________时,△CDF为等腰三角形。
-
科目: 来源: 题型:
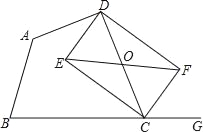
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF平分∠GCD,EF∥BC交CD于点O.
(1)求证:OE=OF;
(2)若点O为CD的中点,求证:四边形DECF是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若有理数x、y,满足|x|=5,|y|=2,且|x+y|=x+y,求x-y的值.
(2)已知a和b互为相反数,c,d互为倒数,|x|=2,求3a+3b-
 - x
- x
相关试题

