Question

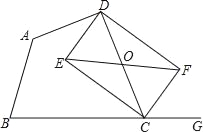
【题目】已知：如图，在四边形ABCD中，点G在边BC的延长线上，CE平分∠BCD，CF平分∠GCD，EF∥BC交CD于点O．

（1）求证：OE=OF；

（2）若点O为CD的中点，求证：四边形DECF是矩形．

Answer 1

【答案】证明见解析

【解析】试题分析：（1）由角平分线的定义及平行线的性质可证得∠DCE=∠FEC，∠EFC=∠DCF，则可求得OE=OC=OF；

（2）利用（1）的结论，结合条件可证得四边形DECF为平行四边形，再利用角平分线的定义可求得∠ECF为直角，则可证得四边形DECF为矩形．

试题解析：解：（1）∵CE平分∠BCD、CF平分∠GCD，∴∠BCE=∠DCE，∠DCF=∠GCF．

∵EF∥BC，∴∠BCE=∠FEC，∠EFC=∠GCF，∴∠DCE=∠FEC，∠EFC=∠DCF，∴OE=OC，OF=OC，∴OE=OF；

（2）∵点O为CD的中点，∴OD=OC．又∵OE=OF，∴四边形DECF是平行四边形．

∵CE平分∠BCD、CF平分∠GCD，∴∠DCE=∠BCD，∠DCF=∠DCG，∴∠DCE+∠DCF=（∠BCD+∠DCG）=90°，即∠ECF=90°，∴四边形DECF是矩形．