【题目】数学课上,老师提出一个问题:如图①,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是
是![]() 轴正半轴上一动点,以
轴正半轴上一动点,以![]() 为边作等腰直角三角形
为边作等腰直角三角形![]() ,使
,使![]() ,点
,点![]() 在第一象限,设点
在第一象限,设点![]() 的横坐标为
的横坐标为![]() ,设……为
,设……为![]() ,
,![]() 与
与![]() 之间的函数图象如图②所示.题中用“……”表示的缺失的条件应补为( )
之间的函数图象如图②所示.题中用“……”表示的缺失的条件应补为( )


A.点![]() 的横坐标B.点
的横坐标B.点![]() 的纵坐标C.
的纵坐标C.![]() 的周长D.
的周长D.![]() 的面积
的面积
参考答案:
【答案】B
【解析】
从图②可以看出,当![]() 时,
时,![]() ,此时点C的纵坐标为1;△ADC≌△BOA(AAS),当
,此时点C的纵坐标为1;△ADC≌△BOA(AAS),当![]() 时,
时,![]() ,即可求解.
,即可求解.
从图②可以看出,当![]() 时,
时,![]() ,
,
此时点C的纵坐标为1;
当![]() 时,过点C作CD⊥y轴于点D,
时,过点C作CD⊥y轴于点D,
∵△ABC是等腰直角三角形,
∴∠BAC=90°,AB=AC,
∵∠DAC+∠ACD=90°,∠DAC+∠OAB=180°-∠BAC=180°-90° =90°,
∴∠OAB=∠DCA,
∠ADC=∠BOA=90°,
∴△ADC≌△BOA(AAS),
∴BO=AD,OA=CD,
则OD=AD+OD=1+2=3,
即:点C纵坐标为3;
∴设点![]() 的横坐标为
的横坐标为![]() ,点C纵坐标为
,点C纵坐标为![]() ,
,
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一个矩形纸片
 ,放置在平面直角坐标系中,
,放置在平面直角坐标系中, ,
,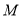 是边
是边 上一点,将
上一点,将 沿直线
沿直线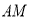 对折,得到
对折,得到 .
.
(1)当
 平分
平分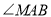 时,求
时,求 的度数和点
的度数和点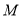 的坐标.
的坐标.(2)连接
 ,当
,当 时,求
时,求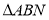 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以O为原点的直角坐标系中,A点的坐标为(0,3),直线x=-3交x轴于点B,P为线段AB上一动点,作直线PC⊥PO,交于直线x=﹣3于点C。过P点作直线MN平行于x轴,交y轴于M,交直线x=﹣3于点N。

(1)当点C在第二象限时,求证:△OPM≌△PCN;
(2)设AP长为m,以P、O、B、C为顶点的四边形的面积为S,请求出S与M之间的函数关系式,并写出自变量m的取值范围;
(3)当点P在线段AB上移动时,点C也随之在直线x=-3上移动,△PBC是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰三角形的点P的坐标,如果不可能,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某款篮球架的示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.26,sin75°≈0.97,tan75°≈3.73,
 ≈1.73)( )
≈1.73)( )
A.3.04
B.3.05
C.3.06
D.4.40 -
科目: 来源: 题型:
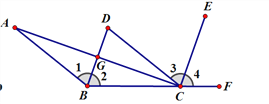
查看答案和解析>>【题目】如图,CD//AB,BD平分∠ABC,CE平分∠DCF,∠ACE=90°
(1)请问BD和CE是否平行?请你说明理由;
(2)AC和BD有何位置关系?请你说明判断的理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,菱形
中,菱形 的顶点
的顶点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,点
,点 在第一象限内,对角线
在第一象限内,对角线 与
与 轴平行,直线
轴平行,直线 与
与 轴、
轴、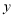 轴分别交于点
轴分别交于点 .将菱形
.将菱形 沿
沿 轴向左平移
轴向左平移 个单位.当点
个单位.当点 落在
落在 的内部时(不包括三角形的边),则
的内部时(不包括三角形的边),则 的取值范围是__________.
的取值范围是__________.
相关试题

