【题目】如图,以O为原点的直角坐标系中,A点的坐标为(0,3),直线x=-3交x轴于点B,P为线段AB上一动点,作直线PC⊥PO,交于直线x=﹣3于点C。过P点作直线MN平行于x轴,交y轴于M,交直线x=﹣3于点N。
(1)当点C在第二象限时,求证:△OPM≌△PCN;
(2)设AP长为m,以P、O、B、C为顶点的四边形的面积为S,请求出S与M之间的函数关系式,并写出自变量m的取值范围;
(3)当点P在线段AB上移动时,点C也随之在直线x=-3上移动,△PBC是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰三角形的点P的坐标,如果不可能,请说明理由。
参考答案:
【答案】
(1)解:略
(2)解: 
(3)解:P1(0,3) P2 ![]()
【解析】(1)由条件先求出点B的坐标,由点A(0,3)可以得出OB=OA,进而可以得出∠ABO=45°,又MN∥x轴,可以得出∠BPN=45°,从而可以得出BN=PN=MO,再由角相等的关系可以得出△OPM≌△PCN;
(2)由∠BAO=45°及PA=m可以求出PM,NC的长度之间的关系,可以求出PN,就可以分为两种情况表示出S的表达式.
(3)当P点在A点PC∥x轴时或PB=BC=3时△PBC是等腰三角形,由条件可以求出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】黄冈市三运会期间,武穴黄商有一种姚明牌运动装每件的销售价y(元)与时间x(周)之间的函数关系式对应的点都在如图所示的图象上,该图象从左至右,依次是线段AB、线段BC、线段CD,而这种运动装每件的进价Z(元)与时间x(周)之间的函数关系式为Z=
 (1≤x≤16且x为整数)
(1≤x≤16且x为整数)
(1)写出每件的销售价y(元)与时间x(周)之间的函数关系式;
(2)设每件运动装销售利润为w,写出w(元)与时间x(周)之间的函数关系式;
(3)求该运动装第几周出销时,每件运动装的销售利润最大?最大利润为多少?(6分) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DC∥FP,∠1=∠2,∠FED=28,∠AGF=80,FH平分∠EFG.
(1)说明:DC∥AB;
(2)求∠PFH的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一个矩形纸片
 ,放置在平面直角坐标系中,
,放置在平面直角坐标系中, ,
,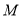 是边
是边 上一点,将
上一点,将 沿直线
沿直线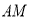 对折,得到
对折,得到 .
.
(1)当
 平分
平分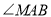 时,求
时,求 的度数和点
的度数和点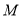 的坐标.
的坐标.(2)连接
 ,当
,当 时,求
时,求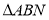 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,老师提出一个问题:如图①,在平面直角坐标系中,点
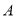 的坐标为
的坐标为 ,点
,点 是
是 轴正半轴上一动点,以
轴正半轴上一动点,以 为边作等腰直角三角形
为边作等腰直角三角形 ,使
,使 ,点
,点 在第一象限,设点
在第一象限,设点 的横坐标为
的横坐标为 ,设……为
,设……为 ,
, 与
与 之间的函数图象如图②所示.题中用“……”表示的缺失的条件应补为( )
之间的函数图象如图②所示.题中用“……”表示的缺失的条件应补为( )

A.点
 的横坐标B.点
的横坐标B.点 的纵坐标C.
的纵坐标C. 的周长D.
的周长D. 的面积
的面积 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某款篮球架的示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.26,sin75°≈0.97,tan75°≈3.73,
 ≈1.73)( )
≈1.73)( )
A.3.04
B.3.05
C.3.06
D.4.40
相关试题

