【题目】如图,平面直角坐标系中,平行四边形![]() 的顶点
的顶点![]() ,边
,边![]() 落在
落在![]() 正半轴上,
正半轴上,![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 分别作
分别作![]() ,
,![]() 交平行四边形各边如图.若反比例函数
交平行四边形各边如图.若反比例函数![]() 的图象经过点
的图象经过点![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,则
,则![]() 的值为__.
的值为__.

参考答案:
【答案】![]()
【解析】
过C作CM⊥x轴于点M,由平行四边形DCOE的面积可求得OE,过D作DN⊥x轴于点N,由C点坐标则可求得ON的长,从而可求得D点坐标,代入反比例函数解析式可求得k的值
如图,过C作CM⊥x轴于点M,过D作DN⊥x轴于点N,则四边形CMND为矩形,
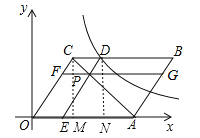
∵四边形OABC为平行四边形,
∴CD∥OE,且DE∥OC,
∴四边形DCOE为平行四边形,
∵C(2,5),
∴OM=2,CM=5,
由图可得,S△AOC=S△ABC=![]() SABCO,
SABCO,
又∵S△FCP=S△DCP且S△AEP=S△AGP,
∴SOEPF=SBGPD,
∵四边形BCFG的面积为10,
∴SCDEO=SBCFG=10,
∴S四边形DCOE=OECM=10,即5OE=10,解得OE=2,
∴CD=MN=2,
∴ON=OM+MN=2+2=4,DN=CM=5,
∴D(4,5),
∵反比例函数y=![]() 图象过点D,
图象过点D,
∴k=4×5=20.
故答案为:20.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,点M为CD中点,将△MBC沿BM翻折至△MBE,若∠AME = α,∠ABE = β,则 α 与 β 之间的数量关系为( )
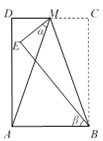
A. α+3β=180° B. β-α=20° C. α+β=80° D. 3β-2α=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD 中,对角线AC,BD交于点O,以 AD,OD为邻边作平行四边形ADOE,连接BE.
(1) 求证:四边形AOBE是菱形;
(2) 若∠EAO+∠DCO=180°,DC=2,求四边形ADOE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 在 数轴上对应的数分别用
在 数轴上对应的数分别用 表示,且
表示,且 .
. 是数轴的一动点.
是数轴的一动点. ⑴在数轴上标出
 的位置,并求出
的位置,并求出 之间的距离;
之间的距离;⑵数轴上一点
 距
距 点24个单位的长度,其对应的数
点24个单位的长度,其对应的数 满足
满足 ,当
,当 点满足
点满足 时,求
时,求 点对应的数.
点对应的数.⑶动点
 从原点开始第一次向左移动1个单位,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,……点
从原点开始第一次向左移动1个单位,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,……点 能移动到与
能移动到与 或
或 重合的位置吗?若能,请探究第几次移动时重合;若不能,请说明理由.
重合的位置吗?若能,请探究第几次移动时重合;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

(1)扇形统计图中“优秀”所对应的扇形的圆心角为 度,并将条形统计图补充完整.
(2)此次比赛有四名同学活动满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了加强学生的安全意识,组织学生参加安全知识竞赛,并从中抽取了部分学生的成绩(得分均为整数,满分100分)进行统计,绘制了两幅尚不完整的统计图如图所示,
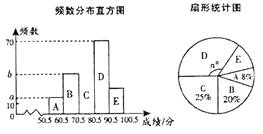
根据统计图中的信息解答下列问题:
(1)若
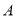 组的频数比
组的频数比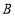 组小
组小 ,则频数分布直方图中
,则频数分布直方图中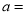 ________,
________,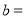 ________;
________;(2)扇形统计图中
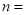 ________,并补全频数分布直方图;
________,并补全频数分布直方图;(3)若成绩在
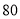 分以上为优秀,全校共有
分以上为优秀,全校共有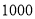 名学生,请估计成绩优秀的学生有多少名?
名学生,请估计成绩优秀的学生有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】小颖和小红两位同学在做投掷骰子(质地均匀的正方体)实验,他们共做了
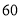 次实验,实验的结果如下:
次实验,实验的结果如下:朝上的点数
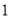
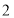
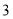
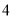
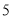
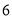
出现的次数
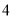
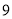
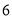
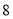
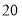
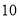
(1)计算“
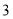 点朝上”的频率和“
点朝上”的频率和“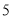 点朝上”的频率.
点朝上”的频率.(2)小颖说:“根据实验得出,出现
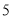 点朝上的机会最大”;小红说:“如投掷
点朝上的机会最大”;小红说:“如投掷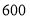 次,那么出现
次,那么出现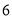 点朝上的次数正好是
点朝上的次数正好是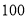 次.”小颖和小红的说法正确吗?为什么?
次.”小颖和小红的说法正确吗?为什么?
相关试题

