【题目】如图,在长方形ABCD中,点M为CD中点,将△MBC沿BM翻折至△MBE,若∠AME = α,∠ABE = β,则 α 与 β 之间的数量关系为( )
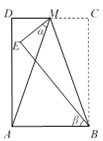
A. α+3β=180° B. β-α=20° C. α+β=80° D. 3β-2α=90°
参考答案:
【答案】D
【解析】
直接利用平行线的性质结合翻折变换的性质得出△ADM≌△BCM(SAS),进而利用直角三角形的性质得出答案.
∵M为CD中点,
∴DM=CM,
在△ADM和△BCM中
∵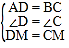 ,
,
∴△ADM≌△BCM(SAS),
∴∠AMD=∠BMC,AM=BM
∴∠MAB=∠MBA
∵将点C绕着BM翻折到点E处,
∴∠EBM=∠CBM,∠BME=∠BMC=∠AMD
∴∠DME=∠AMB
∴∠EBM=∠CBM=![]() (90°-β)
(90°-β)
∴∠MBA=![]() (90°-β)+ β=
(90°-β)+ β=![]() (90°+β)
(90°+β)
∴∠MAB=∠MBA=![]() (90°+β)
(90°+β)
∴∠DME=∠AMB=180°-∠MAB-∠MBA=90°-β
∵长方形ABCD中,
∴CD∥AB
∴∠DMA=∠MAB=![]() (90°+β)
(90°+β)
∴∠DME+∠AME=∠ABE+∠MBE
∵∠AME=α,∠ABE=β,
∴90°-β+α=β+![]() (90°-β)
(90°-β)
∴3β-2α=90°
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

-
科目: 来源: 题型:
查看答案和解析>>【题目】某开发商进行商铺促销,广告上写着如下条款:投资者购买商铺后,必须由开发商代租赁5年,5年期满后由开发商以比原商铺标价高20%的价格进行回购,投资者可在以下两种购铺方案中做出选择:
方案一:按照商铺标价一次性付清铺款,每年可获得的租金为商铺标价的10%;
方案二:按商铺标价的八折一次性付清铺款,前3年商铺的租金收益归开发商所有,3年后每年可获得的租金为商铺标价的9%
(1)问投资者选择哪种购铺方案,5年后所获得的投资收益率更高?为什么?
(注:投资收益率=
 ×100%)
×100%)(2)对同一标价的商铺,甲选择了购铺方案一,乙选择了购铺方案二,那么5年后两人获得的收益相差7.2万元.问甲乙两人各投资了多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD 中,对角线AC,BD交于点O,以 AD,OD为邻边作平行四边形ADOE,连接BE.
(1) 求证:四边形AOBE是菱形;
(2) 若∠EAO+∠DCO=180°,DC=2,求四边形ADOE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 在 数轴上对应的数分别用
在 数轴上对应的数分别用 表示,且
表示,且 .
. 是数轴的一动点.
是数轴的一动点. ⑴在数轴上标出
 的位置,并求出
的位置,并求出 之间的距离;
之间的距离;⑵数轴上一点
 距
距 点24个单位的长度,其对应的数
点24个单位的长度,其对应的数 满足
满足 ,当
,当 点满足
点满足 时,求
时,求 点对应的数.
点对应的数.⑶动点
 从原点开始第一次向左移动1个单位,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,……点
从原点开始第一次向左移动1个单位,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,……点 能移动到与
能移动到与 或
或 重合的位置吗?若能,请探究第几次移动时重合;若不能,请说明理由.
重合的位置吗?若能,请探究第几次移动时重合;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,平行四边形
 的顶点
的顶点 ,边
,边 落在
落在 正半轴上,
正半轴上, 为线段
为线段 上一点,过点
上一点,过点 分别作
分别作 ,
, 交平行四边形各边如图.若反比例函数
交平行四边形各边如图.若反比例函数 的图象经过点
的图象经过点 ,四边形
,四边形 的面积为
的面积为 ,则
,则 的值为__.
的值为__.
相关试题

