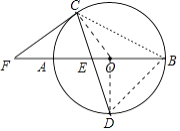
【题目】如图,AB是⊙O的直径,点C为AB上面半圆上一点,点D为AB的下面半圆的中点,连接CD与AB交于点E,延长BA至F,使EF=CF. 
(1)求证:CF与⊙O相切;
(2)若DEDC=13,求⊙O的半径.
参考答案:
【答案】
(1)解:连接OC、OD.
∵ ![]() =
= ![]() ,
,
∴OD⊥AB,∠AOD=90°,
∵FE=FC,
∴∠FCE=∠FEC,
∵OC=OD,
∴∠OCE=∠ODC,
∴∠FCO=∠FCE+∠OCE=∠FEC+∠EDO=∠OED+∠ODC=90°.
∴OC⊥CF,
∴CF是⊙⊙O的切线
(2)解:连接BC、BD.

∵ ![]() =
= ![]() ,
,
∠EBD=∠BCD,
∵∠BDE=∠CDB,
∴△BDE∽△CDB,
∴ ![]() =
= ![]() ,
,
∴BD2=CDED=13,
∵∠BOD=90°,
∴OB2+OD2=BD2=13,
∴OB2= ![]() ,
,
∴OB= ![]() ,
,
∴⊙O的半径为 ![]()
【解析】(1)欲证明CF与⊙O相切,只要证明OC⊥CF即可.(2)由△BDE∽△CDB,推出 ![]() =
= ![]() ,推出BD2=CDED=12,由∠BOD=90°,推出OB2+OD2=BD2=12,推出OB2=6,可得OB=
,推出BD2=CDED=12,由∠BOD=90°,推出OB2+OD2=BD2=12,推出OB2=6,可得OB= ![]() 解决问题.
解决问题.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣(2m+1)x+m(m+1)=0
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两根分别为x1、x2 , 求x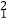 +x
+x  的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备购进一批排球和篮球,已知1个排球和2个篮球共需320元,3个排球和1个篮球共需360元.
(1)求一个排球和一个篮球的售价各是多少元?
(2)学校准备购进这种排球和篮球共40个,且篮球的数量不少于排球数量的3倍,求最省钱的购买方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AE平分∠BAD交BC于点E.
(1)作CF平分∠BCD交AD于点F(用尺规作图,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,求证:△ABE≌△CDF.

-
科目: 来源: 题型:
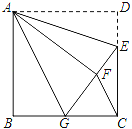
查看答案和解析>>【题目】如图,正方形ABCD中,CD=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
(1)求证:△ABG≌△AFG;
(2)求GC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,在平面直角坐标系中,抛物线y=ax2+3x+c与x轴交于A、B两点,与y轴交于点C(0,8),直线l经过原点O,与抛物线的一个交点为D(6,8).
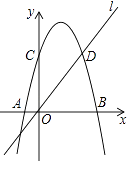
(1)求抛物线的解析式;
(2)抛物线的对称轴与直线l交于点E,点T为x轴上方的抛物线上的一个动点.
①当∠TEC=∠TEO时,求点T的坐标;
②直线BT与y轴交于点P,与直线l交于点Q,当OP=OQ时,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于代数式x2-10x+24,下列说法:①它是二次三项式; ②该代数式的值可能等于2017;③分解因式的结果是(x-4)(x-6);④该代数式的值可能小于-1.其中正确的有( )
A.1个
B.2个
C.3 个
D.4个
相关试题

