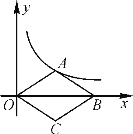
【题目】如图,在平面直角坐标系中,点O为原点,反比例函数y=![]() 的图象经过点(1,4),菱形OABC的顶点A在函数的图象上,对角线OB在x轴上.
的图象经过点(1,4),菱形OABC的顶点A在函数的图象上,对角线OB在x轴上.
(1)求反比例函数的关系式;
(2)直接写出菱形OABC的面积.
参考答案:
【答案】(1) y=![]() .(2)8.
.(2)8.
【解析】(1)把(1,4)代入y=![]() ,可求出k;(2) 连对角线,一个小三角形面积是2,一共4个全等三角形,所以面积为8.
,可求出k;(2) 连对角线,一个小三角形面积是2,一共4个全等三角形,所以面积为8.
解:(1)因为反比例函数y=![]() 的图象经过点(1,4),所以4=
的图象经过点(1,4),所以4=![]() ,即k=4.
,即k=4.
所以反比例函数的关系式为y=![]() .
.
(2) 连接AC交x轴于点D,
∵四边形OABC是菱形,
∴AD=CD,AD⊥OB,OD=BD,
∴S△AOD=S△ABD=S△OCD=S△BCD,
∵S△OAD=![]() ×4=2,
×4=2,
∴S菱形OABC=8.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某天猫店销售某种规格学生软式排球,成本为每个30元.以往销售大数据分析表明:当每只售价为40元时,平均每月售出600个;若售价每上涨1元,其月销售量就减少20个,若售价每下降1元,其月销售量就增加200个.
(1)若售价上涨m元,每月能售出 个排球(用m的代数式表示).
(2)为迎接“双十一”,该天猫店在10月底备货1300个该规格的排球,并决定整个11月份进行降价促销,问售价定为多少元时,能使11月份这种规格排球获利恰好为8400元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC内接于⊙O,BC是⊙O的直径,点D是BC延长线上的一点,AD=AB,且∠ACB=2∠D,CD=2(如图1)

(1)求证:AD是⊙O的切线;
(2)AD= ;
(3)若点E是⊙O上的一点,AE与BC交于点F,且点E等分半圆BC时(如图2),求CF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
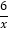 (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.(1) 求一次函数的表达式;
(2) 根据图象写出kx+b-
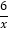 <0的x的取值范围.
<0的x的取值范围.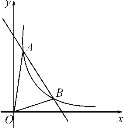
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y1=ax+b与反比例函数y2=
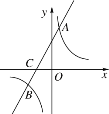
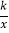 交于A,B两点,与x轴交于点C,点A的纵坐标为6,点B的坐标为(-3,-2).
交于A,B两点,与x轴交于点C,点A的纵坐标为6,点B的坐标为(-3,-2).(1)求直线和反比例函数的解析式;
(2)求点C的坐标,并结合图象直接写出y1<0时x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
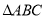 的顶点
的顶点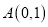 ,
,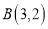 ,
,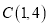 均在正方形网格的格点上.
均在正方形网格的格点上.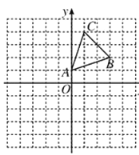
(1)画出
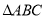 关于
关于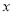 轴对称的图形
轴对称的图形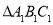 ;
;(2)已知
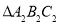 和
和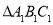 关于
关于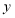 轴成轴对称,写出顶点
轴成轴对称,写出顶点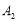 ,
,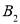 ,
,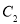 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一次函数y=kx+b与反比例函数y=
 的图象交于A(2,4),B(﹣4,n)两点.
的图象交于A(2,4),B(﹣4,n)两点.(1)分别求出一次函数与反比例函数的表达式;
(2)过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.

相关试题

