【题目】△ABC内接于⊙O,BC是⊙O的直径,点D是BC延长线上的一点,AD=AB,且∠ACB=2∠D,CD=2(如图1)

(1)求证:AD是⊙O的切线;
(2)AD= ;
(3)若点E是⊙O上的一点,AE与BC交于点F,且点E等分半圆BC时(如图2),求CF的长.
参考答案:
【答案】(1)详见解析;(2)![]() ;(3)CF=
;(3)CF=![]() .
.
【解析】
(1)连接OA,通过证明AD⊥OA即可得出结论;
(2)易得△OAC是等边三角形,可得CA=OC=OA=CD=2,由勾股定理得AD的长;
(3)过F作FH⊥AC,H为垂足,设CH=x,在Rt△CFH中求得FH=![]() ,在Rt△AFH中,求得AH =
,在Rt△AFH中,求得AH =![]() ,由AH+GH=2求得x的值,从而得出结论.
,由AH+GH=2求得x的值,从而得出结论.
(1)连结OA,
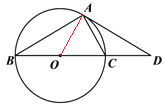
∵AD=AB,
∴∠ B=∠D
∵∠ACB=2∠D
∴∠ACB=2∠B
∵BC是⊙O的直径,
∴∠BAC=90°
在Rt△ABC中, ∠B+∠ACB=90°,即∠B=30°,∠D=30°,∠BAD=120°
又∵OA=OB,
∴∠OAB=∠B=30°,
∴∠OAD=90°
即AD⊥OA ,
∴AD是⊙O的切线
(2)∵OA=OC, ∠ACB =2∠D =60,△OAC是等边三角形,
∴AC=OC,
∠OAC =60,∠CAD =30=∠D,
∴CA=OC=OA=CD=2
在Rt△OAD中, ![]()
(3)过F作FH⊥AC,H为垂足,
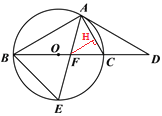
设CH=x,在Rt△CFH中,∠ACF =60,FH=![]() ,
,
在Rt△AFH中,∠FAH =45,
∴AH=FH=![]() ,
,
又AC=CD=2,
∴![]() ,
,
![]() ,
,
∴CF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出无鱼水缸内最高水位
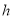 与注水时间
与注水时间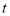 之间的变化情况的是( )
之间的变化情况的是( )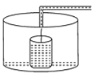
A.
 B.
B.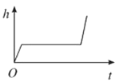
C.
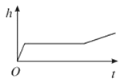 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M的表示的数为________________.
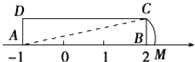
【答案】
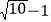
【解析】AC=AM=
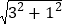 =
= ,∴AM=
,∴AM=
【题型】填空题
【结束】
11【题目】在△ABC中,AB=10,AC=2
 ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】某天猫店销售某种规格学生软式排球,成本为每个30元.以往销售大数据分析表明:当每只售价为40元时,平均每月售出600个;若售价每上涨1元,其月销售量就减少20个,若售价每下降1元,其月销售量就增加200个.
(1)若售价上涨m元,每月能售出 个排球(用m的代数式表示).
(2)为迎接“双十一”,该天猫店在10月底备货1300个该规格的排球,并决定整个11月份进行降价促销,问售价定为多少元时,能使11月份这种规格排球获利恰好为8400元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
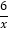 (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.(1) 求一次函数的表达式;
(2) 根据图象写出kx+b-
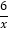 <0的x的取值范围.
<0的x的取值范围.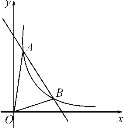
-
科目: 来源: 题型:
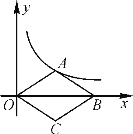
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为原点,反比例函数y=
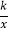 的图象经过点(1,4),菱形OABC的顶点A在函数的图象上,对角线OB在x轴上.
的图象经过点(1,4),菱形OABC的顶点A在函数的图象上,对角线OB在x轴上.(1)求反比例函数的关系式;
(2)直接写出菱形OABC的面积.
-
科目: 来源: 题型:
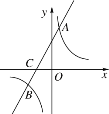
查看答案和解析>>【题目】如图,直线y1=ax+b与反比例函数y2=
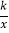 交于A,B两点,与x轴交于点C,点A的纵坐标为6,点B的坐标为(-3,-2).
交于A,B两点,与x轴交于点C,点A的纵坐标为6,点B的坐标为(-3,-2).(1)求直线和反比例函数的解析式;
(2)求点C的坐标,并结合图象直接写出y1<0时x的取值范围.
相关试题

