【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(﹣1,1)且经过点B,连接AB,直线AB与此抛物线的另一个交点为C,则S△BCD:S△ABO=( )

A.8:1
B.6:1
C.5:1
D.4:1
参考答案:
【答案】B
【解析】
试题分析:设直线AB的解析式为y=kx+b,二次函数的解析式为y=a(x+1)2+1,
将点A(1,0)、B(0,2)代入y=kx+b中得:
![]() ,解得:
,解得:![]() ,
,
∴直线AB的解析式为y=﹣2x+2;
将点B(0,2)代入到y=a(x+1)2+1中得:
2=a+1,解得:a=1,
∴二次函数的解析式为y=(x+1)2+1=x2+2x+2.
将y=﹣2x+2代入y=x2+2x+2中得:
﹣2x+2=x2+2x+2,整理得:x2+4x=0,
解得:x1=﹣4,x2=0,
∴点C的坐标为(﹣4,10).
∵点C(﹣4,10),点B(0,2),点A(1,0),
∴AB=![]() ,BC=
,BC=![]() ,
,
∴BC=4AB.
∵直线AB解析式为y=﹣2x+2可变形为2x+y﹣2=0,
∴|﹣2+1﹣2|=3,|﹣2|=2.
∴S△BCD:S△ABO=4×3:2=12:2=6:1.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积. 例如,由1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
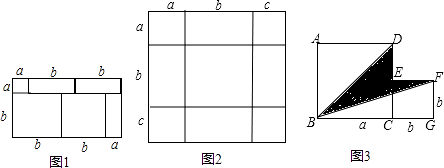
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个角的补角是它的余角的4倍,求这个角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点C是线段AB上的一点,如果线段AC=8cm,线段BC=4cm,则线段AC和BC的中点间的距离为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点C是线段AB上的一点,如果线段AC=8cm,线段BC=4cm,则线段AC和BC的中点间的距离为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:0﹣2018=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算或变形中,不正确的是( )
A.a2a5=a10B.a2﹣2ab+b2=(a﹣b)2
C.ab2﹣4ab+4a=a(b﹣2)2D.3a3b2÷a2b2=3a
相关试题

