搜索
【题目】当k取不同的值时，y关于x的函数y=kx+2（k≠0）的图象为总是经过点（0，2）的直线，我们把所有这样的直线合起来，称为经过点（0，2）的“直线束”．那么，下面经过点（﹣1，2）的直线束的函数式是（ ）
A. y=kx﹣2（k≠0） B. y=kx+k+2（k≠0）
C. y=kx﹣k+2（k≠0） D. y=kx+k﹣2（k≠0）
参考答案：
【答案】B
【解析】
把已知点（﹣1，2）代入选项所给解析式进行判断即可．
在y=kx﹣2中，当x=﹣1时，y=﹣k﹣2≠2，故A选项不合题意，
在y=kx+k+2中，当x=﹣1时，y=﹣k+k+2=2，故B选项符合题意，
在y=kx﹣k+2中，当x=﹣1时，y=﹣k﹣k﹣2=﹣2k﹣2≠2，故C选项不合题意，
在y=kx+k﹣2中，当x=﹣1时，y=﹣k+k﹣2=﹣2≠2，故D选项不合题意，
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】求值：
（1）已知x﹣2的平方根是±2，2x+y+7的立方根是3，求x2+y2的平方根．
（2）已知实数a、b满足（a﹣2）2+
=0，求b﹣a的算术平方根（3）已知y=
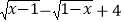，求
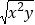的值 -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，O为原点，直线y=kx+b交x轴于A（﹣3，0），交y轴于B，且三角形AOB的面积为6，则k=（ ）
A.
B. ﹣ C. ﹣4或4 D. ﹣或 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知等边△ABC，请用直尺（不带刻度）和圆规，按下列要求作图（不要求写作法，但要保留作图痕迹）：
（1）作△ABC的外心O；
（2）设D是AB边上一点，在图中作出一个正六边形DEFGHI，使点F，点H分别在边BC和AC上． -
科目： 来源： 题型：
查看答案和解析>>【题目】操作：“如图1，P是平面直角坐标系中一点（x轴上的点除外），过点P作PC⊥x轴于点C，点C绕点P逆时针旋转60°得到点Q．”我们将此由点P得到点Q的操作称为点的T变换．
（1）点P（a，b）经过T变换后得到的点Q的坐标为
；若点M经过T变换后得到点N（6，﹣ 
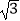），则点M的坐标为 ．
（2）A是函数y=
x图象上异于原点O的任意一点，经过T变换后得到点B．
①求经过点O，点B的直线的函数表达式；
②如图2，直线AB交y轴于点D，求△OAB的面积与△OAD的面积之比． -
科目： 来源： 题型：
查看答案和解析>>【题目】某地新建的一个企业，每月将生产1960吨污水，为保护环境，该企业计划购置污水处理器，并在如下两个型号种选择：
污水处理器型号
A型
B型
处理污水能力（吨/月）
240
180
已知商家售出的2台A型、3台B型污水处理器的总价为44万元，售出的1台A型、4台B型污水处理器的总价为42万元．
（1）求每台A型、B型污水处理器的价格；
（2）为确保将每月产生的污水全部处理完，该企业决定购买上述的污水处理器，那么他们至少要支付多少钱？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以原点O为圆心，3为半径的圆与x轴分别交于A，B两点（点B在点A的右边），P是半径OB上一点，过P且垂直于AB的直线与⊙O分别交于C，D两点（点C在点D的上方），直线AC，DB交于点E．若AC：CE=1：2．
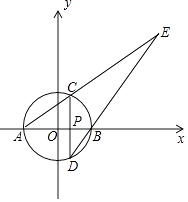
（1）求点P的坐标；
（2）求过点A和点E，且顶点在直线CD上的抛物线的函数表达式．
相关试题
