搜索
【题目】在平面直角坐标系中，O为原点，直线y=kx+b交x轴于A（﹣3，0），交y轴于B，且三角形AOB的面积为6，则k=（ ）
A. 
B. ﹣ C. ﹣4或4 D. ﹣或
参考答案：
【答案】D
【解析】
由S△AOB=6可得
OA|yB|=6，据此求得yB=4或yB=﹣4，从而得出点B的坐标，再利用待定系数法分别求得函数解析式．
∵A（﹣3，0），
∴OA=3，
由S△AOB=6可得OA|yB|=6，即×3×|yB|=6，
解得：yB=4或yB=﹣4，
则点B的坐标为（0，4）或（0，﹣4），
当点B坐标为（0，4）时，把A、B坐标代入y=kx+b，
可得：
，解得：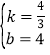
；
当点B的坐标为（0，﹣4）时，把A、B坐标代入y=kx+b，
可得：
，解得：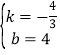
；
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙、丙、丁四人玩扑克牌游戏，他们先取出两张红心和两张黑桃共四张扑克牌，洗匀后背面朝上放在桌面上，每人抽取其中一张，拿到相同颜色的即为游戏搭档，现甲、乙两人各抽取了一张，求两人恰好成为游戏搭档的概率．（请用“画树状图”或“列表”等方法写出分析过程）
-
科目： 来源： 题型：
查看答案和解析>>【题目】在正方形网格中，我们把，每个小正方形的顶点叫做格点，连接任意两个格点的线段叫网格线段，以网格线段为边组成的图形叫做格点图形，在下列如图所示的正方形网格中，每个小正方形的边长为1．
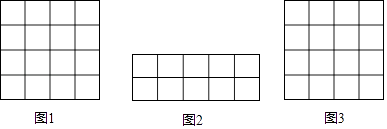
（1）请你在图1中画一个格点图形，且该图形是边长为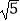
的菱形；
（2）请你在图2中用网格线段将其切割成若干个三角形和正方形，拼接成一个与其面积相等的正方形，并在图3中画出格点正方形． -
科目： 来源： 题型：
查看答案和解析>>【题目】求值：
（1）已知x﹣2的平方根是±2，2x+y+7的立方根是3，求x2+y2的平方根．
（2）已知实数a、b满足（a﹣2）2+
=0，求b﹣a的算术平方根（3）已知y=
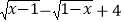，求
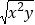的值 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知等边△ABC，请用直尺（不带刻度）和圆规，按下列要求作图（不要求写作法，但要保留作图痕迹）：
（1）作△ABC的外心O；
（2）设D是AB边上一点，在图中作出一个正六边形DEFGHI，使点F，点H分别在边BC和AC上． -
科目： 来源： 题型：
查看答案和解析>>【题目】当k取不同的值时，y关于x的函数y=kx+2（k≠0）的图象为总是经过点（0，2）的直线，我们把所有这样的直线合起来，称为经过点（0，2）的“直线束”．那么，下面经过点（﹣1，2）的直线束的函数式是（ ）
A. y=kx﹣2（k≠0） B. y=kx+k+2（k≠0）
C. y=kx﹣k+2（k≠0） D. y=kx+k﹣2（k≠0）
-
科目： 来源： 题型：
查看答案和解析>>【题目】操作：“如图1，P是平面直角坐标系中一点（x轴上的点除外），过点P作PC⊥x轴于点C，点C绕点P逆时针旋转60°得到点Q．”我们将此由点P得到点Q的操作称为点的T变换．
（1）点P（a，b）经过T变换后得到的点Q的坐标为
；若点M经过T变换后得到点N（6，﹣ 
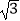），则点M的坐标为 ．
（2）A是函数y=
x图象上异于原点O的任意一点，经过T变换后得到点B．
①求经过点O，点B的直线的函数表达式；
②如图2，直线AB交y轴于点D，求△OAB的面积与△OAD的面积之比．
相关试题
