【题目】如图,在平面直角坐标系中,点C(﹣3,0),点A,B分别在x轴,y轴的正半轴上,且满足 ![]() +|OA﹣1|=0
+|OA﹣1|=0
(1)求点A,点B的坐标.
(2)若点P从C点出发,以每秒1个单位的速度沿射线CB运动,连结AP.设△ABP的面积为S,点P的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点P,使以点A,B,P为顶点的三角形与△AOB相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:∵ ![]() +|OA﹣1|=0
+|OA﹣1|=0
∴OA﹣1=0、OB2﹣3=0,
∴OA=1、OB= ![]() ,
,
∴点A的坐标为(1,0)、B的坐标(0, ![]() )
)

(2)解:∵C(﹣3,0),B(0, ![]() );
);
∴OC=3,OB= ![]()
在RT△BOC中,BC= ![]() =2
=2 ![]() ,
,
设点A到直线CB的距离为y,则
![]() ×2
×2 ![]() y=
y= ![]() ×(3+1)×
×(3+1)× ![]() ,
,
解得y=2.
则S= ![]() ×|2
×|2 ![]() ﹣t|×2=|2
﹣t|×2=|2 ![]() ﹣t|.
﹣t|.
故S与t的函数关系式为:S=﹣t+2 ![]() (0≤t≤2
(0≤t≤2 ![]() )或S=t﹣2
)或S=t﹣2 ![]() (t>2
(t>2 ![]() ).
).
(3)解:存在,
理由:∵tan∠OBC= ![]() =
= ![]() =
= ![]() ,
,
∴∠OBC=60°,
∴∠BCO=30°,
∴BC=2OB=2 ![]() ,
,
∵tan∠OBA= ![]() =
= ![]() =
= ![]() ,
,
∴∠OBA=30°,
∴∠ABC=90°,AB=2OA=2,
①当0≤t≤2 ![]() 时,若△PBA∽△AOB时,则
时,若△PBA∽△AOB时,则 ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴PB= ![]() ,
,
∴PBsin60°= ![]() ×
× ![]() =1,PBcos60°=
=1,PBcos60°= ![]() ×
× ![]() =
= ![]() ,
,
∴P(﹣1, ![]() );
);
若△ABP∽△AOB时,则 ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴PB=2 ![]() ,
,
∴PBsin60°=2 ![]() ×
× ![]() =3,PBcos60°=2
=3,PBcos60°=2 ![]() ×
× ![]() =
= ![]() ,
,
∴P(﹣3,0),
②当t>2 ![]() 时,若△PBA∽△AOB时,则
时,若△PBA∽△AOB时,则 ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴PB= ![]() ,
,
∴PBsin60°= ![]() ×
× ![]() =1,PBcos60°=
=1,PBcos60°= ![]() ×
× ![]() =
= ![]() ,
,
∴P(1, ![]() );
);
若△ABP∽△AOB时,则 ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴PB=2 ![]() ,
,
∴PBsin60°=2 ![]() ×
× ![]() =3,PBcos60°=2
=3,PBcos60°=2 ![]() ×
× ![]() =
= ![]() ,
,
∴P(3,2 ![]() ),
),
所以,存在点P,使以点A,B,P为顶点的三角形与△AOB相似,P点的坐标为(﹣1, ![]() )或(﹣3,0)或(1,
)或(﹣3,0)或(1, ![]() )或(3,2
)或(3,2 ![]() ).
).
【解析】(1)根据非负数的和为0,每个数均为0,得到OA、OB的长,即可求出答案;(2)根据勾股定理得到CB的长度,再根据三角形面积公式即可得到点A到直线CB的距离;再根据△ABP的面积=![]() BP
BP![]() AB,用t的代数式表示BP即|
AB,用t的代数式表示BP即|![]() ﹣t|,即可得到S与t的函数关系式由于是射线CB,可分为P在线段CB上和在CB延长线上两种情况;(3)先求得∠ABC=90°,然后分两种情况讨论:①当0≤t≤
﹣t|,即可得到S与t的函数关系式由于是射线CB,可分为P在线段CB上和在CB延长线上两种情况;(3)先求得∠ABC=90°,然后分两种情况讨论:①当0≤t≤![]() ②当t>
②当t>![]() , 利用对应边成比例列出方程,再运用三角函数,即可求得点P的坐标.
, 利用对应边成比例列出方程,再运用三角函数,即可求得点P的坐标.
【考点精析】关于本题考查的三角形的面积和勾股定理的概念,需要了解三角形的面积=1/2×底×高;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角三角形ABC的直角边AB=6,BC=8,将直角三角形ABC沿边BC的方向平移到三角形DEF的位置,DE交AC于点G,BE=2,三角形CEG的面积为13.5,下列结论:
①三角形ABC平移的距离是4; ②EG=4.5;
③AD∥CF; ④四边形ADFC的面积为6.
其中正确的结论是( )

A. ①② B. ②③ C. ③④ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,三角形ABC的顶点坐标分别为
 ,
, ,
, ,把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形
,把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形 .
. (1)画出三角形ABC和平移后
 的图形;
的图形;(2)写出三个顶点
 ,
, ,
, 的坐标;
的坐标;(3)求三角形ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△
 和△
和△ 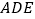 都是等腰直角三角形,
都是等腰直角三角形,  ,
,  ,
,  ,
,  是
是  的中点.若将△
的中点.若将△ 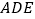 绕点
绕点  旋转一周,则线段
旋转一周,则线段  长度的取值范围是( )
长度的取值范围是( )
A.
B.
C.
D.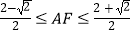
-
科目: 来源: 题型:
查看答案和解析>>【题目】请你补全证明过程:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:EF∥CD

证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=90°,∠ACB=90°①( )
∴∠DGB=∠ACB ②( )
∴DG∥AC ③( )
∴∠2= ④________ ⑤( )
又∠1=∠2 ⑥( )
∴∠1=∠DCA ⑦( )
∴EF∥CD ⑧( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】记面积为18cm2的平行四边形的一条边长为x(cm),这条边上的高线长为y(cm).
(1)写出y关于x的函数表达式及自变量x的取值范围;
(2)在如图直角坐标系中,用描点法画出所求函数图象;
(3)若平行四边形的一边长为4cm,一条对角线长为
 cm,请直接写出此平行四边形的周长.
cm,请直接写出此平行四边形的周长.
相关试题

