【题目】已知△ ![]() 和△
和△ ![]() 都是等腰直角三角形,
都是等腰直角三角形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是 ![]() 的中点.若将△
的中点.若将△ ![]() 绕点
绕点 ![]() 旋转一周,则线段
旋转一周,则线段 ![]() 长度的取值范围是( )
长度的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】A
【解析】根据旋转的特性,画出E点旋转一圈的轨迹,如图:

结合图形可知:
①当E落在E′位置时,AF最大,
∵△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,AC=2 ![]() ,AD=1,
,AD=1,
∴AB= ![]() =4, AE=AE'=
=4, AE=AE'= ![]() =
= ![]() , BE'=ABAE′=4
, BE'=ABAE′=4 ![]() ,
,
∵F是BE′的中点,
∴BF= ![]() BE′=
BE′= ![]() , AF=ABBF=4
, AF=ABBF=4 ![]() =
= ![]() ;
;
②当E落在E″位置时,AF最小,
∵BE″=AB+AE″=4+ ![]() ,且F是BE″的中点,
,且F是BE″的中点,
∴BF= ![]() BE″=
BE″= ![]() ,
,
AF=ABBF=4 ![]() =
= ![]() .
.
综合①②可知: ![]() AF
AF ![]()
故A符合题意.
故答案为:A.
根据题意画出图形,可知当E落在E′位置时,AF最大;当E落在E″位置时,AF最小.然后根据等腰直角三角形的性质求出AF的取值,可得其范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,三角形ABC的顶点坐标分别为
 ,
, ,
, ,把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形
,把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形 .
. (1)画出三角形ABC和平移后
 的图形;
的图形;(2)写出三个顶点
 ,
, ,
, 的坐标;
的坐标;(3)求三角形ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点C(﹣3,0),点A,B分别在x轴,y轴的正半轴上,且满足
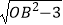 +|OA﹣1|=0
+|OA﹣1|=0
(1)求点A,点B的坐标.
(2)若点P从C点出发,以每秒1个单位的速度沿射线CB运动,连结AP.设△ABP的面积为S,点P的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点P,使以点A,B,P为顶点的三角形与△AOB相似?若存在,请直接写出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】请你补全证明过程:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:EF∥CD

证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=90°,∠ACB=90°①( )
∴∠DGB=∠ACB ②( )
∴DG∥AC ③( )
∴∠2= ④________ ⑤( )
又∠1=∠2 ⑥( )
∴∠1=∠DCA ⑦( )
∴EF∥CD ⑧( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】记面积为18cm2的平行四边形的一条边长为x(cm),这条边上的高线长为y(cm).
(1)写出y关于x的函数表达式及自变量x的取值范围;
(2)在如图直角坐标系中,用描点法画出所求函数图象;
(3)若平行四边形的一边长为4cm,一条对角线长为
 cm,请直接写出此平行四边形的周长.
cm,请直接写出此平行四边形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是半径为
是半径为 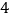 的⊙
的⊙  的直径,
的直径,  是圆上异于
是圆上异于  ,
,  的任意一点,
的任意一点,  的平分线交⊙
的平分线交⊙  于点
于点  ,连接
,连接  和
和  ,△
,△  的中位线所在的直线与⊙
的中位线所在的直线与⊙  相交于点
相交于点  、
、  ,则
,则 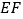 的长是.
的长是.
相关试题

