【题目】阅读下面的解题过程: 已知 ![]() =
= ![]() ,求
,求 ![]() 的值.
的值.
解:由 ![]() =
= ![]() 知x≠0,所以
知x≠0,所以 ![]() =2,即x+
=2,即x+ ![]() =2.
=2.
∴ ![]() =x2+
=x2+ ![]() =(x+
=(x+ ![]() )2﹣2=22﹣2=2,故
)2﹣2=22﹣2=2,故 ![]() 的值为
的值为 ![]()
评注:该题的解法叫做“倒数法”,请你利用“倒数法”解下面的题目:
已知 ![]() =
= ![]() ,求
,求 ![]() 的值.
的值.
参考答案:
【答案】解:∵ ![]() =
= ![]() , ∴
, ∴ ![]() =7,
=7,
x+ ![]() =8,
=8,
∵ ![]() =x2+
=x2+ ![]() =(x+
=(x+ ![]() )2﹣2=82﹣2=62,
)2﹣2=82﹣2=62,
∴ ![]() =
= ![]()
【解析】首先根据解答例题可得 ![]() =7,进而可得x+
=7,进而可得x+ ![]() =8,再求
=8,再求 ![]() 的倒数的值,进而可得答案.
的倒数的值,进而可得答案.
【考点精析】根据题目的已知条件,利用分式的混合运算的相关知识可以得到问题的答案,需要掌握运算的顺序:第一级运算是加法和减法;第二级运算是乘法和除法;第三级运算是乘方.如果一个式子里含有几级运算,那么先做第三级运算,再作第二级运算,最后再做第一级运算;如果有括号先做括号里面的运算.如顺口溜:"先三后二再做一,有了括号先做里."当有多层括号时,先算括号内的运算,从里向外{[(?)]}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=90°,∠COD=30°.
(1)如图1,当点O、A、C在同一条直线上时,∠BOD的度数是;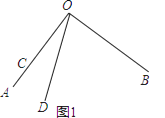
(2)将∠COD从图1的位置开始,绕点O逆时针方向旋转n°(即∠AOC=n°),且0<n<180.
①如果∠COD的一边与∠AOB的一边垂直,则n= .
②当60<n<90时(如图2),作射线OM平分∠AOC,射线ON平分∠BOD,试求∠MON的度数 .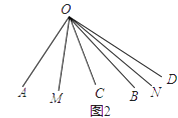
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两地相距450千米,一辆快车和一辆慢车上午7点分别从甲、乙两地以不变的速度同时出发开往乙地和甲地,快车到达乙地后休息一个小时按原速返回,快车返回甲地时已是下午5点,慢车在快车前一个小时到达甲地.试根据以上信息解答以下问题:
(1)分别求出快车、慢车的速度(单位:千米/小时);
(2)从两车出发直至慢车达到甲地的过程中,经过几小时两车相距150千米. -
科目: 来源: 题型:
查看答案和解析>>【题目】若x=﹣1是方程x2+px+q=0的解,则p﹣q的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.
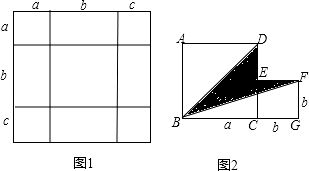
(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来.
(2)如图2,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠AOB的边OB上的一点.
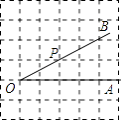
(1)过点P画OB的垂线,交OA于点C,
(2)过点P画OA的垂线,垂足为H,
(3)线段PH的长度是点P到的距离,线段是点C到直线OB的距离.
(4)因为直线外一点到直线上各点连接的所有线中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是(用“<”号连接) -
科目: 来源: 题型:
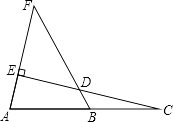
查看答案和解析>>【题目】如图,C在AB的延长线上,CE⊥AF于E,交FB于D,若∠F=40°,∠C=20°,则∠FBA的度数为( )
A.50°
B.60°
C.70°
D.80°
相关试题

