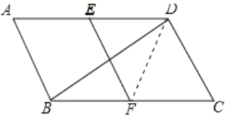
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)求![]() 的长.
的长.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】
(1)由平行四边形的性质得出AD∥BC,AD=BC,证出DE∥CF,DE=CF,得出四边形CDEF是平行四边形,证出CD=CF,即可得出四边形CDEF是菱形;
(2)连接DF,证明△CDF是等边三角形,得出∠CDF=∠CFD=60°,求出∠BDF=30°,证出∠BDC=∠BDF+∠CDF=90°,由勾股定理即可得出答案.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵E,F分别是AD,BC的中点,
∴DE=![]() AD,CF=
AD,CF=![]() BC,
BC,
∴DE∥CF,DE=CF,
∴四边形CDEF是平行四边形,
又∵BC=2CD,
∴CD=CF,
∴四边形CDEF是菱形;
(2)如图,连接![]() ,
,
![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,![]() .
.
![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数
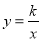 (k<0)的图象经过点A(-1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到了点B’在此反比例函数的图象上,则t的值是( )
(k<0)的图象经过点A(-1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到了点B’在此反比例函数的图象上,则t的值是( )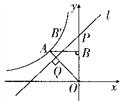
A.
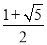 B.
B. 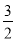 C.
C. 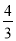 D.
D. 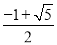
-
科目: 来源: 题型:
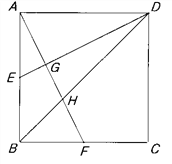
查看答案和解析>>【题目】正方形ABCD中,E,F分别是AB与BC边上的中点,连接AF,DE,BD,交于G,H(如图所示)。求AG:GH:HF的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
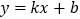 的图象与反比例函数
的图象与反比例函数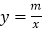 的图象交于
的图象交于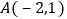 ,
,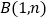 两点.
两点. Ⅰ
Ⅰ 试确定上述反比例函数和一次函数的表达式;
试确定上述反比例函数和一次函数的表达式; Ⅱ
Ⅱ 连OB,在x轴上取点C,使
连OB,在x轴上取点C,使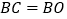 ,并求
,并求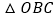 的面积;
的面积; Ⅲ
Ⅲ 直接写出一次函数值大于反比例函数值的自变量x的取值范围.
直接写出一次函数值大于反比例函数值的自变量x的取值范围.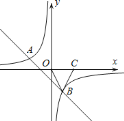
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好治理河流水质,保护环境,某市治污公司决定购买10台污水处理设备,现有A,B两种型号的设备,其中每台的价格,月处理污水量如表:
A型
B型
价格(万元/台)
a
b
处理污水量(吨/月)
220
180
经调查:购买一台A型设备比购买一台B型设备多3万元,购买2台A型设备比购买3台B型设备少3万元.
(1)求a,b的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过100万元,你认为该公司有哪几种购买方案;
(3)在(2)问的条件下,若每月要求处理的污水量不低于1880吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2016年5月1日起对居民生活用电试行新的“阶梯电价”收费,具体收费标准如表:
一户居民一个月用电量的范围
电费价格(单位:元/千瓦时)
不超过150千瓦时的部分
a
超过150千瓦时,但不超过300千瓦时的部分
b
超过300千瓦时的部分
a+0.5
2016年5月份,该市居民甲用电200千瓦时,交费170元;居民乙用电400千瓦时,交费400元.
(1)求上表中a、b的值:
(2)试行“阶梯电价”收费以后,该市一户居民月用电多少千瓦时,其当月的平均电价每千瓦时不超过0.85元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90,E为AB的中点,求证:
(1)AC2=AB·AD;
(2)CE∥AD。

相关试题

