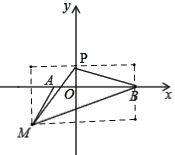
【题目】如图,在平面直角坐标系中,已知点A(﹣1,0),点B(3,0).在第三象限内有一点M(﹣2,m).
(1)请用含m的式子表示△ABM的面积;
(2)当m=-![]() 时,在y轴上有一点P,使△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使△BMP的面积与△ABM的面积相等,请求出点P的坐标.

参考答案:
【答案】(1)-2m;(2)点P坐标是(0,﹣![]() )或(0,
)或(0,![]() ).
).
【解析】
(1)过M作CE⊥x轴于E,根据点M在第三象限可得ME=-m,根据A、B坐标可求出AB的长,利用三角形面积公式即可得答案;(2)先根据(1)计算S△ABM,再分两种情况:当点P在y轴正半轴上时、当点P在y轴负半轴上时,利用割补法表示出S△BMP,根据S△BMP=S△ABM列方程求解可得.
(1)如图1所示,过M作CE⊥x轴于E,
∵A(﹣1,0),B(3,0),
∴OA=1,OB=3,
∴AB=4,
∵在第三象限内有一点M(﹣2,m),
∴ME=|m|=﹣m,
∴S△ABM=![]() AB×ME=
AB×ME=![]() ×4×(﹣m)=﹣2m;
×4×(﹣m)=﹣2m;
(2)当m=-![]() 时,M(-2,-
时,M(-2,-![]() )
)
∴S△ABM=-2×(-![]() )=3,
)=3,
点P有两种情况:
①当点P在y轴正半轴上时,设点p(0,k)
S△BMP=5×(![]() +k)-
+k)-![]() ×2×(
×2×(![]() +k)-
+k)-![]() ×5×
×5×![]() -
-![]() ×3×k=
×3×k=![]() k+
k+![]() ,
,
∵S△BMP=S△ABM,
∴![]() k+
k+![]() =3,
=3,
解得:k=![]() ,
,
∴点P坐标为(0,![]() );
);
②当点P在y轴负半轴上时,设点p(0,n),
S△BMP=-5n-![]() ×2×(-n-
×2×(-n-![]() )-
)-![]() ×5×
×5×![]() -
-![]() ×3×(-n)=-
×3×(-n)=-![]() n-
n-![]() ,
,
∵S△BMP=S△ABM,
∴-![]() n-
n-![]() =3,
=3,
解得:n=﹣![]()
∴点P坐标为(0,﹣![]() ),
),
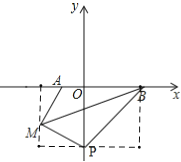
故点P的坐标为(0,![]() )或(0,﹣
)或(0,﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条直线上依次有A、B、C三地,自行车爱好者甲、乙两人同时分别从A、B两地出发,沿直线匀速骑向C地.已知甲的速度为20 km/h,设甲、乙两人行驶x(h)后,与A地的距离分别为y1 、y2 (km), y1 、y2 与x的函数关系如图所示.
(1)求y2与x的函数关系式;
(2)若两人在出发时都配备了通话距离为3km的对讲机,求甲、乙两人在骑行过程中可以用对讲机通话的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的沙县﹣﹣我最喜爱的沙县小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图.

请根据所给信息解答以下问题:
(1)请补全条形统计图;
(2)在一个不透明的口袋中有4个完全相同的小球,把它们分别标号为四种小吃的序号A,B,C,D.随机地摸出一个小球然后放回,再随机地摸出一个小球.请用列表或画树状图的方法,求出两次都摸到A的概率.
(3)近几年,沙县小吃产业发展良好,给沙县经济带来了发展.2011年底,小吃产业年营业额达50亿元,到了2013年底,小吃产业年营业额达60.5亿元.假设每年的小吃产业年营业额平均增长率不变,求这两年平均增长率是多少?(数据来源于网络)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b分别交y轴、x轴于C、D两点,与反比例函数y=
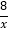 (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣
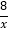 <0的x的取值范围;
<0的x的取值范围;(3)求△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆⊙O的直径,BC是⊙O的切线,连结AC交⊙O于点D,E为
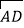 上一点,连结AE、BE,BE交AC于点F,且AE2=EFEB
上一点,连结AE、BE,BE交AC于点F,且AE2=EFEB(1)求证:CB=CF.
(2)若点E到弦AD的距离为1,cos∠C=
 ,求⊙O的半径.
,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD⊥BC于D,AD=BD,AC=BE.
(1)求证:∠BED=∠C;
(2)猜想并说明BE和AC有什么数量和位置关系。

相关试题

