【题目】如图,AB是圆⊙O的直径,BC是⊙O的切线,连结AC交⊙O于点D,E为![]() 上一点,连结AE、BE,BE交AC于点F,且AE2=EFEB
上一点,连结AE、BE,BE交AC于点F,且AE2=EFEB
(1)求证:CB=CF.
(2)若点E到弦AD的距离为1,cos∠C=![]() ,求⊙O的半径.
,求⊙O的半径.

参考答案:
【答案】(1)证明见解析;(2)⊙O的半径是![]() .
.
【解析】
(1)如图1,由已知证明△AEF∽△BEA,根据相似三角形的对应角相等可得∠1=∠EAB,再根据∠1=∠2,∠3=∠EAB,从而可得∠2=∠3,继而可得CB=CF;
(2)如图2,连接OE交AC于点G,设⊙O的半径是r,由(1)可得∠4=∠5,继而可得![]() ,从而可得EG=1,根据cos∠C=
,从而可得EG=1,根据cos∠C=![]() ,且∠C+∠GAO=90°,可得sin∠GAO=
,且∠C+∠GAO=90°,可得sin∠GAO=![]() ,继而可求得半径长.
,继而可求得半径长.
(1)如图1,∵AE2=EFEB,
∴![]() ,
,
又∵∠AEF=∠AEB,
∴△AEF∽△BEA,
∴∠1=∠EAB.
∵∠1=∠2,∠3=∠EAB,
∴∠2=∠3,
∴CB=CF;
(2)如图2,连接OE交AC于点G,设⊙O的半径是r,
由(1)知,△AEF∽△BEA,则∠4=∠5,
∴![]() ,
,
∴OE⊥AD,
∴EG=1,
∵cos∠C=![]() ,且∠C+∠GAO=90°,
,且∠C+∠GAO=90°,
∴sin∠GAO=![]() ,
,
∴![]() ,即
,即![]() ,
,
解得,r=![]() ,
,
即⊙O的半径是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的沙县﹣﹣我最喜爱的沙县小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图.

请根据所给信息解答以下问题:
(1)请补全条形统计图;
(2)在一个不透明的口袋中有4个完全相同的小球,把它们分别标号为四种小吃的序号A,B,C,D.随机地摸出一个小球然后放回,再随机地摸出一个小球.请用列表或画树状图的方法,求出两次都摸到A的概率.
(3)近几年,沙县小吃产业发展良好,给沙县经济带来了发展.2011年底,小吃产业年营业额达50亿元,到了2013年底,小吃产业年营业额达60.5亿元.假设每年的小吃产业年营业额平均增长率不变,求这两年平均增长率是多少?(数据来源于网络)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(﹣1,0),点B(3,0).在第三象限内有一点M(﹣2,m).
(1)请用含m的式子表示△ABM的面积;
(2)当m=-
 时,在y轴上有一点P,使△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使△BMP的面积与△ABM的面积相等,请求出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b分别交y轴、x轴于C、D两点,与反比例函数y=
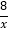 (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣
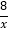 <0的x的取值范围;
<0的x的取值范围;(3)求△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD⊥BC于D,AD=BD,AC=BE.
(1)求证:∠BED=∠C;
(2)猜想并说明BE和AC有什么数量和位置关系。

-
科目: 来源: 题型:
查看答案和解析>>【题目】一位运动员在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离是2.5m时,达到最大高度3.5m,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式.
(2)该运动员身高1.8m,在这次跳投中,球在头顶上0.25m处出手,
问:球出手时,他距离地面的高度是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AD=3,CD=4,点E在CD上,且DE=1.



(1)感知:如图①,连接AE,过点E作EF丄AE,交BC于点F,连接AE,易证:△ADE≌△ECF(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE和△ECF相似;
(3)应用:如图③,若EF交AB于点F,EF丄PE,其他条件不变,且△PEF的面积是6,则AP的长为_____.
相关试题

