搜索
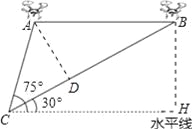
【题目】某兴趣小组借助无人飞机航拍校园．如图，无人飞机从A处水平飞行至B处需8秒，在地面C处同一方向上分别测得A处的仰角为75°，B处的仰角为30°．已知无人飞机的飞行速度为4米/秒，求这架无人飞机的飞行高度．（结果保留根号）
参考答案：
【答案】8+8
【解析】试题分析：如图，作AD⊥BC，BH⊥水平线，根据题意确定出∠ABC与∠ACB的度数，利用锐角三角函数定义求出AD与BD的长，由CD+BD求出BC的长，即可求出BH的长．
试题解析：如图，作AD⊥BC，BH⊥水平线，
由题意得：∠ACH=75°，∠BCH=30°，AB∥CH，
∴∠ABC=30°，∠ACB=45°，
∵AB=32m，
∴AD=CD=16m，BD=ABcos30°=
m，
∴BC=CD+BD=（
+16）m，
则BH=BCsin30°=
m，
答：这架无人飞机的飞行高度为
m．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我市某中学有一块四边形的空地ABCD，如图所示，为了绿化环境，学校计划在空地上种植草皮，经测量∠A=90°，AB=3m，DA=4m，BC=12m，CD=13m．
（1）求出空地ABCD的面积．
（2）若每种植1平方米草皮需要200元，问总共需投入多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将边长为4的正方形置于平面直角坐标系第一象限，使AB边落在x轴正半轴上，且点A的坐标是（1，0）．
（1）直线y＝
x﹣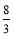
经过点C，且与x轴交于点E，求四边形AECD的面积；（2）若直线l经过点E，且将正方形ABCD分成面积相等的两部分，求直线l的函数表达式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一条直线上依次有A、B、C三地，自行车爱好者甲、乙两人同时分别从A、B两地出发，沿直线匀速骑向C地．已知甲的速度为20 km/h，设甲、乙两人行驶x（h）后，与A地的距离分别为y1 、y2 （km）， y1 、y2 与x的函数关系如图所示．
（1）求y2与x的函数关系式；
（2）若两人在出发时都配备了通话距离为3km的对讲机，求甲、乙两人在骑行过程中可以用对讲机通话的时间．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的沙县﹣﹣我最喜爱的沙县小吃”调查活动，将调查问卷整理后绘制成如图所示的不完整条形统计图．
请根据所给信息解答以下问题：
（1）请补全条形统计图；
（2）在一个不透明的口袋中有4个完全相同的小球，把它们分别标号为四种小吃的序号A，B，C，D．随机地摸出一个小球然后放回，再随机地摸出一个小球．请用列表或画树状图的方法，求出两次都摸到A的概率．
（3）近几年，沙县小吃产业发展良好，给沙县经济带来了发展.2011年底，小吃产业年营业额达50亿元，到了2013年底，小吃产业年营业额达60.5亿元．假设每年的小吃产业年营业额平均增长率不变，求这两年平均增长率是多少？（数据来源于网络）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知点A（﹣1，0），点B（3，0）．在第三象限内有一点M（﹣2，m）．
(1)请用含m的式子表示△ABM的面积；
(2)当m＝-
时，在y轴上有一点P，使△BMP的面积与△ABM的面积相等，请求出点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=kx+b分别交y轴、x轴于C、D两点，与反比例函数y=
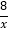（x＞0）的图象交于A（m，8），B（4，n）两点．（1）求一次函数的解析式；
（2）根据图象直接写出kx+b﹣
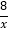＜0的x的取值范围；（3）求△AOB的面积．
相关试题
