【题目】如图,在Rt△ABC中,∠ACB=90,以AC为直径作 ![]() 交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
(1)求证:DE是 ![]() 的切线;
的切线;
(2)若CF=2,DF=4,求 ![]() 直径的长.
直径的长.
参考答案:
【答案】
(1)证明:如图,连接OD、CD.
∵AC为 ![]() 的直径,
的直径,
∴△BCD是直角三角形,
∵E为BC的中点,
∴BE=CE=DE,∴∠CDE=∠DCE,
∵OD=OC,
∴∠ODC=∠OCD,
∵∠ACB=90°,
∴∠OCD+∠DCE=90°,
∴∠ODC+∠CDE=90°,即OD⊥DE,
∴DE是 ![]() 的切线;
的切线;
(2)解:设⊙O的半径为 ![]() ,
,
∵∠ODF=90°,∴ ![]() ,
,
即 ![]() ,解得:
,解得: ![]() ,
,
∴ ![]() 的直径为6.
的直径为6.
【解析】(1)连接OD、CD;易由圆周角定理的推论,可得△BCD是直角三角形,由E为BC的中点,直角三角形斜边上的中线等于斜边的一半,易得BE=CE=DE,∠CDE=∠DCE;又由半径OD=OC,可得∠ODC=∠OCD,利用等量代换可得∠BCA=90°,切线得证。
(2)易由(1)可得∠ODF=90°利用勾股定理可得半径r=3,所以直径为6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究:如图①,在△ABC 中,∠BAC=90°,AB=AC,直线 m 经过点 A,BD⊥m 于点 D,CE⊥m 于点 E,求证:△ABD≌△CAE.
应用:如图②,在△ABC 中,AB=AC,D、A、E 三点都在直线 m 上,并且有∠BDA=∠AEC=∠BAC,求证:DE=BD+CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数分别填入相应的集合中:-(-230),
 ,0,-0.99,1.31,5,
,0,-0.99,1.31,5, ,3.14246792…,-
,3.14246792…,- .
.(1)整数集合:{ …}
(2)非正数集合:{ …}
(3)正有理数集合:{ …}
(4)无理数集合:{ …}
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,直线a∥直线b,点A、D在直线a上,点B、C在直线b上,连接AB、AC、BD、DC,得△ABC和△BDC,△ABC的面积_______△BDC的面积(填“>”、“=”或“<”).
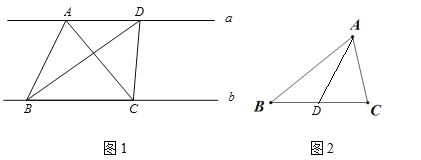

(2)如图2,已知△ABC,过点A有一条线段,将△ABC的面积平分,且交BC于点D,则
 .
.(3)如图3,已知四边形ABCD,请过点D作一条线段DG将四边形ABCD面积平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】芳芳同学手中有一块长方形纸板和一块正方形纸板,其中长方形纸板的长为3 dm,宽为2 dm,且两块纸板的面积相等.
(1)求正方形纸板的边长(结果保留根号).
(2)芳芳能否在长方形纸板上截出两个完整的,且面积分别为2 dm2和3 dm2的正方形纸板?判断并说明理由.(提示:
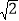 ≈1.414,
≈1.414,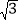 ≈1.732)
≈1.732) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,△DAC和△DBE都是等边三角形.

(1)求证:△DAB≌△DCE;
(2)求证:DA∥EC. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是将抛物线
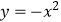 平移后得到的抛物线,其对称轴为
平移后得到的抛物线,其对称轴为 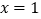 ,与x轴的一个交点为A
,与x轴的一个交点为A 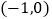 ,另一交点为B,与y轴交点为C.
,另一交点为B,与y轴交点为C.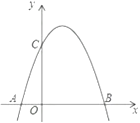
(1)求抛物线的函数表达式;
(2)若点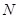 为抛物线上一点,且BC⊥NC,求点N的坐标;
为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数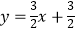 的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
相关试题

