【题目】探究:如图①,在△ABC 中,∠BAC=90°,AB=AC,直线 m 经过点 A,BD⊥m 于点 D,CE⊥m 于点 E,求证:△ABD≌△CAE.
应用:如图②,在△ABC 中,AB=AC,D、A、E 三点都在直线 m 上,并且有∠BDA=∠AEC=∠BAC,求证:DE=BD+CE.

参考答案:
【答案】证明见解析
【解析】
(1)根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90![]() ,而∠BAC=90
,而∠BAC=90![]() ,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断△ADB≌△CEA.则AE=BD,AD=CE,于是DE=AE+AD=BD+CE;
,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断△ADB≌△CEA.则AE=BD,AD=CE,于是DE=AE+AD=BD+CE;
(2)利用∠BDA=∠BAC=α,则∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,得出∠CAE=∠ABD,进而得出△ADB≌△CEA即可得出答案.
证明:(1)∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
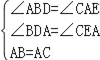 ,
,
∴△ADB≌△CEA(AAS);
(2)设∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
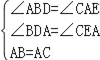 ,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在结束了380课时初中阶段数学内容的教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制如下统计图表(图1~图3),请根据图表提供的信息,回答下列问题:

(1)图1中“统计与概率”所在扇形的圆心角为 度;
(2)图2、3中的a= ,b= ;
(3)在60课时的总复习中,唐老师应安排多少课时复习“数与代数”内容?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在
 点上正方
点上正方  的
的  处发出一球,羽毛球飞行的高度
处发出一球,羽毛球飞行的高度  与水平距离
与水平距离  之间满足函数表达式
之间满足函数表达式  .已知点
.已知点  与球网的水平距离为
与球网的水平距离为  ,球网的高度为
,球网的高度为  .
.
(1)当 时,①求
时,①求  的值;②通过计算判断此球能否过网;
的值;②通过计算判断此球能否过网;
(2)若甲发球过网后,羽毛球飞行到 处时,乙扣球成功。已知点
处时,乙扣球成功。已知点  离点
离点  的水平距离为
的水平距离为  ,离地面的高度为
,离地面的高度为  的,求
的,求  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数分别填入相应的集合中:-(-230),
 ,0,-0.99,1.31,5,
,0,-0.99,1.31,5, ,3.14246792…,-
,3.14246792…,- .
.(1)整数集合:{ …}
(2)非正数集合:{ …}
(3)正有理数集合:{ …}
(4)无理数集合:{ …}
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,直线a∥直线b,点A、D在直线a上,点B、C在直线b上,连接AB、AC、BD、DC,得△ABC和△BDC,△ABC的面积_______△BDC的面积(填“>”、“=”或“<”).
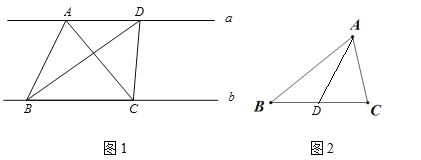

(2)如图2,已知△ABC,过点A有一条线段,将△ABC的面积平分,且交BC于点D,则
 .
.(3)如图3,已知四边形ABCD,请过点D作一条线段DG将四边形ABCD面积平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90,以AC为直径作
 交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
(1)求证:DE是 的切线;
的切线;
(2)若CF=2,DF=4,求 直径的长.
直径的长.
相关试题

