【题目】建设银行的某储蓄员小张在办理业务时,约定存入为正,取出为负.![]() 年
年![]() 月
月![]() 日他办理了
日他办理了![]() 件业务:
件业务:![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元.
元.
![]() 若他早上领取备用金
若他早上领取备用金![]() 元,那么下班时应交回银行多少元?
元,那么下班时应交回银行多少元?
![]() 若每办一件业务,银行发给业务量的
若每办一件业务,银行发给业务量的![]() 作为奖励,那么这天小张应得奖金多少元?
作为奖励,那么这天小张应得奖金多少元?
参考答案:
【答案】(1) 他下班时应交回银行![]() 元;(2) 这天他应得奖金为
元;(2) 这天他应得奖金为![]() 元
元
【解析】
(1)存入为正,取出为负,他办理了6件业务:﹣780元、﹣650元、+1250元、﹣310元、﹣420元、+240元.将这几笔业务数额相加的值,再加上领取的备用金5000元,就是下班时应交回银行的钱;
(2)若每办一件业务,银行发给业务量的0.1%作为奖励,那么这天小张应得的奖金就是每笔业务量的绝对值的和0.1%.
(1)5000﹣780﹣650+1250﹣310﹣420+240=4330(元);
答:他下班时应交回银行4330元;
(2)(780+650+1250+310+420+240)×0.1%=3.65(元)
答:这天他应得奖金为3.65元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学中,有许多关系都是在不经意间被发现的.当然,没有敏锐的观察力是做不到的.数学家们往往是这样来研究问题的:特值探究–猜想归纳–逻辑证明–总结应用.下面我们也来像数学家们那样分四步找出这两个代数式的关系:对于代数式
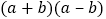 与
与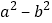 .
.
 特值探究:
特值探究:当
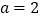 ,
,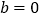 时,
时,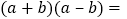 ________;
________;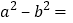 ________
________当
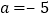 ,
,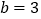 时,
时,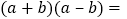 ________;
________;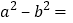 ________
________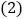 猜想归纳:
猜想归纳:观察
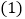 的结果,写出
的结果,写出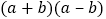 与
与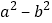 的关系:________.
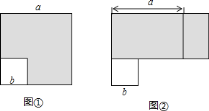
的关系:________. 逻辑证明:如图,边长为
逻辑证明:如图,边长为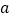 的正方形纸片剪出一个边长为
的正方形纸片剪出一个边长为 的小正方形之后,剩余部分(即阴影部分)又剪拼成一个矩形(不重叠无缝隙),请你说说是如何用这个图来得出
的小正方形之后,剩余部分(即阴影部分)又剪拼成一个矩形(不重叠无缝隙),请你说说是如何用这个图来得出 中的关系?
中的关系? 总结应用:利用你发现的关系,求:
总结应用:利用你发现的关系,求:①若
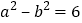 ,且
,且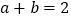 ,则
,则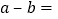 ________;
________;②
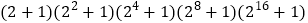 的值.(提示:你可能要用到公式
的值.(提示:你可能要用到公式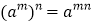 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某大众汽车经销商在销售某款汽车时,以高出进价20%标价.已知按标价的九折销售这款汽车9辆与将标价直降0.2万元销售4辆获利相同.
(1)求该款汽车的进价和标价分别是多少万元?
(2)若该款汽车的进价不变,按(1)中所求的标价出售,该店平均每月可售出这款汽车20辆;若每辆汽车每降价0.1万元,则每月可多售出2辆.求该款汽车降价多少万元出售每月获利最大?最大利润是多少? -
科目: 来源: 题型:
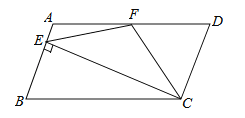
查看答案和解析>>【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上(E不与A、B重合),连接EF、CF,则下列结论中一定成立的是 ( )
①∠DCF=
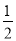 ∠BCD;②EF=CF;③
∠BCD;②EF=CF;③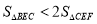 ;④∠DFE=4∠AEF.
;④∠DFE=4∠AEF.A. ①②③④ B. ①②③ C. ①② D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解学生孝敬父母的情况(选项:A为父母洗一次脚;B帮父母做一次家务;C给父母买一件礼物;D其它),在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):
根据以上信息解答下列问题:


(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
(3)该校有1600名学生,估计该校全体学生中选择B选项的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小梅将边长分别为
 ,
, ,
, ,
, ,
, ,
, …长的若干个正方形按一定规律拼成不同的长方形,如图所示.
…长的若干个正方形按一定规律拼成不同的长方形,如图所示. 求第四个长方形的周长;
求第四个长方形的周长; 当
当 时,求第五个长方形的面积.(用科学记数法表示)
时,求第五个长方形的面积.(用科学记数法表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】蜗牛从某点
 开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):
开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米): ,
, ,
, ,
, ,
, ,
, ,
, .
. 通过计算说明蜗牛是否回到起点
通过计算说明蜗牛是否回到起点 .
. 蜗牛离开出发点
蜗牛离开出发点 最远时是多少厘米?
最远时是多少厘米? 在爬行过程中,如果每爬
在爬行过程中,如果每爬 厘米奖励
厘米奖励 粒芝麻,则蜗牛一共得到多少粒芝麻?
粒芝麻,则蜗牛一共得到多少粒芝麻?
相关试题

