【题目】蜗牛从某点![]() 开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):
开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 通过计算说明蜗牛是否回到起点
通过计算说明蜗牛是否回到起点![]() .
.
![]() 蜗牛离开出发点
蜗牛离开出发点![]() 最远时是多少厘米?
最远时是多少厘米?
![]() 在爬行过程中,如果每爬
在爬行过程中,如果每爬![]() 厘米奖励
厘米奖励![]() 粒芝麻,则蜗牛一共得到多少粒芝麻?
粒芝麻,则蜗牛一共得到多少粒芝麻?
参考答案:
【答案】蜗牛一共得到![]() 粒芝麻.
粒芝麻.
【解析】
(1)分别相加,看是否为0,为0则回到了起点O;
(2)分别计算绝对值,再比较大小即可;
(3)计算绝对值的和,就是总路程,列式可得结论.
(1)﹣6+12﹣10+5﹣3+10﹣8=0.
所以蜗牛可以回到起点O.
(2)|﹣6|=6,|﹣6+12|=6,|﹣6+12﹣10|=4,|﹣6+12﹣10+5|=1,|﹣6+12﹣10+5﹣3|=2,|﹣6+12﹣10+5﹣3+10|=8,所以蜗牛离开出发点O最远时是8厘米;
(3)(6+12+10+5+3+10+8)×2=54×2=108
答:蜗牛一共得到108粒芝麻.
-
科目: 来源: 题型:
查看答案和解析>>【题目】建设银行的某储蓄员小张在办理业务时,约定存入为正,取出为负.
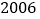 年
年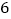 月
月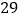 日他办理了
日他办理了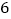 件业务:
件业务: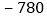 元、
元、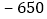 元、
元、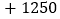 元、
元、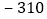 元、
元、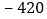 元、
元、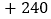 元.
元.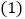 若他早上领取备用金
若他早上领取备用金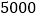 元,那么下班时应交回银行多少元?
元,那么下班时应交回银行多少元? 若每办一件业务,银行发给业务量的
若每办一件业务,银行发给业务量的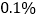 作为奖励,那么这天小张应得奖金多少元?
作为奖励,那么这天小张应得奖金多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解学生孝敬父母的情况(选项:A为父母洗一次脚;B帮父母做一次家务;C给父母买一件礼物;D其它),在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):
根据以上信息解答下列问题:


(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
(3)该校有1600名学生,估计该校全体学生中选择B选项的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小梅将边长分别为
 ,
, ,
, ,
, ,
, ,
, …长的若干个正方形按一定规律拼成不同的长方形,如图所示.
…长的若干个正方形按一定规律拼成不同的长方形,如图所示. 求第四个长方形的周长;
求第四个长方形的周长; 当
当 时,求第五个长方形的面积.(用科学记数法表示)
时,求第五个长方形的面积.(用科学记数法表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°.点D是直线BC上的一个动点,连接AD,并以AD为边在AD的右侧作等边△ADE.

(1)如图①,当点E恰好在线段BC上时,请判断线段DE和BE的数量关系,并结合图①证明你的结论;
(2)当点E不在直线BC上时,连接BE,其它条件不变,(1)中结论是否成立?若成立,请结合图②给予证明;若不成立,请直接写出新的结论;
(3)若AC=3,点D在直线BC上移动的过程中,是否存在以A、C、D、E为顶点的四边形是梯形?如果存在,直接写出线段CD的长度;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,
(1)写出数轴上点B表示的数 ;
(2)|5﹣3|表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离.试探索:
①:若|x﹣8|=2,则x= .
②:|x+12|+|x﹣8|的最小值为 .
(3)动点P从O点出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.求当t为多少秒时?A,P两点之间的距离为2;
(4)动点P,Q分别从O,B两点,同时出发,点P以每秒5个单位长度沿数轴向右匀速运动,Q点以P点速度的两倍,沿数轴向右匀速运动,设运动时间为t(t>0)秒.问当t为多少秒时?P,Q之间的距离为4.
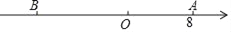
-
科目: 来源: 题型:
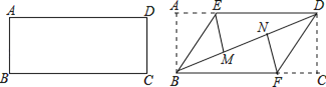
查看答案和解析>>【题目】准备一张矩形纸片,按如图操作:将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.
(1)求证:四边形BFDE是平行四边形.
(2)若四边形BFDE是菱形,BE =2,求菱形BFDE的面积.
相关试题

