【题目】综合题
(1)如图(1),将一副直角三角板的直角顶点C叠放在一起.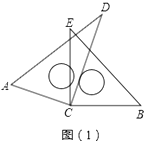
①填空:∠ACE∠BCD(选填“<”或“>”或“=”);
②若∠DCE=25°,求∠ACB的度数;
③猜想∠ACB与∠DCE的数量关系,并说明理由.
(2)若改变(1)中一个三角板的位置,如图(2)所示,则上述第③题的结论是否仍然成立?(不需要说明理由)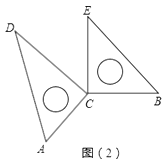
参考答案:
【答案】
(1)=,若∠DCE=25°,∠ACD=90°,所以∠ACE=∠ACD-∠DCE=90°-25°=65°,因为∠BCE=90°且∠ACB=∠ACE+∠BCE,∠ACB=90°+65°=155°;,猜想∠ACB+∠DCE=180°.理由如下:因为∠ACD=90°=∠ECB,∠ACD+∠ECB+∠ACB+∠DCE=360°,所以∠ECD+∠ACB=360°-(∠ACD+∠ECB)=360°-180°=180°
(2)解:成立
【解析】(1)解:∠ACB+∠ECD=180![]() ,理由如下:
,理由如下:
因为∠ACD=∠BCE=90°,
∠ACB+∠ECD=360![]() -∠ACD-∠BCE=180
-∠ACD-∠BCE=180![]()
所以;∠ACB+∠ECD=180![]() .
.
(1)①根据同角的余角相等即可得出结论;②由∠ACE=∠ACD-∠DCE算出∠ACE的度数,由∠BCE=90°且∠ACB=∠ACE+∠BCE算出∠ACB的度数;③猜想∠ACB+∠DCE=180° ,理由如下:由∠ACD=90°=∠ECB,∠ACD+∠ECB+∠ACB+∠DCE=360°,及∠ECD+∠ACB=360°-(∠ACD+∠ECB)得出结论;
(2)根据∠ACD=∠BCE=90°及∠ACB+∠ECD=360![]() -∠ACD-∠BCE就可以得出结论。
-∠ACD-∠BCE就可以得出结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( )
A. 两条对角线互相平分的四边形是平行四边形
B. 两条对角线互相垂直的四边形是菱形
C. 两条对角线互相垂直且相等的四边形是正方形
D. 两条对角线相等的四边形是矩形
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程ax2+4x+2=0有两个相等的实数根,则a的值是( )
A.﹣2B.0C.1D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①,图②,图③都是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,在图③中已画出点A.按下列要求画图:
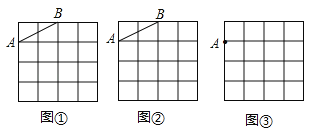
(1)在图①中,以格点为顶点,AB为一边画一个等腰三角形;
(2)在图②中,以格点为顶点,AB为一边画一个正方形;
(3)在图③中,以点A为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是正方形ABCD对角线BD上一点,EM⊥BC,EN⊥CD垂足分别是求M、N

(1)求证:AE=MN;
(2)若AE=2,∠DAE=30°,求正方形的边长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,4秒后,两点相距16个单位长度.已知点B的速度是点A的速度的3倍(速度单位:单位长度/秒).
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动4秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,再过几秒时,原点恰好处在AB的中点?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从原点O位置出发向B点运动,且C的速度是点A的速度的一半;当点C运动几秒时,C为AB的中点?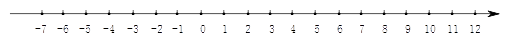
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,∠CBF=20°.
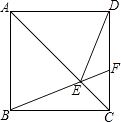
(1)∠ACB的大小=(度);
(2)求证:△ABE≌△ADE;
(3)∠AED的大小=(度).
相关试题

