【题目】如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,∠CBF=20°. 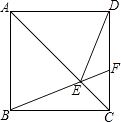
(1)∠ACB的大小=(度);
(2)求证:△ABE≌△ADE;
(3)∠AED的大小=(度).
参考答案:
【答案】
(1)45
(2)证明:∵四边形ABCD是正方形,
∴AB=AD,∠EAB=∠EAD,
在△EAB和△EAD中,
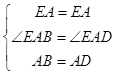 ,
,
∴△EAB≌△EAD.
(3)65
【解析】(1)解:∵四边形ABCD是正方形, ∴∠BCD=90°,∠ACB= ![]() BCD=
BCD= ![]() ×90°=45°.
×90°=45°.
所以答案是45.
(3.)解:∵△EAB≌△EAD,
∴∠AED=∠AEB,
∵∠AEB=∠EBC+∠BCE=20°+45°=65°.
∴∠AED=65°.
所以答案是65.
【考点精析】本题主要考查了正方形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)如图(1),将一副直角三角板的直角顶点C叠放在一起.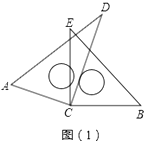
①填空:∠ACE∠BCD(选填“<”或“>”或“=”);
②若∠DCE=25°,求∠ACB的度数;
③猜想∠ACB与∠DCE的数量关系,并说明理由.
(2)若改变(1)中一个三角板的位置,如图(2)所示,则上述第③题的结论是否仍然成立?(不需要说明理由)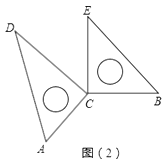
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是正方形ABCD对角线BD上一点,EM⊥BC,EN⊥CD垂足分别是求M、N

(1)求证:AE=MN;
(2)若AE=2,∠DAE=30°,求正方形的边长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,4秒后,两点相距16个单位长度.已知点B的速度是点A的速度的3倍(速度单位:单位长度/秒).
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动4秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,再过几秒时,原点恰好处在AB的中点?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从原点O位置出发向B点运动,且C的速度是点A的速度的一半;当点C运动几秒时,C为AB的中点?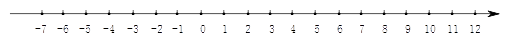
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下午四点半钟的时候,时针和分针所夹的角度是( )
A. 30度 B. 45度 C. 60度 D. 75度
-
科目: 来源: 题型:
查看答案和解析>>【题目】某陶瓷商,为了促销决定卖一只茶壶,赠一只茶杯。某人共付款162元,买得茶壶茶杯共36只,已知每只茶壶15元,每只茶杯3元,问其中茶壶、茶杯各多少只?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2﹣b2=8,且a﹣b=﹣4,则a+b=_____.
相关试题

