【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,4秒后,两点相距16个单位长度.已知点B的速度是点A的速度的3倍(速度单位:单位长度/秒).
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动4秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,再过几秒时,原点恰好处在AB的中点?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从原点O位置出发向B点运动,且C的速度是点A的速度的一半;当点C运动几秒时,C为AB的中点?![]()
参考答案:
【答案】
(1)解:设A的速度是x,则B的速度为3x,由题意,
得:4(x+3x)=16,解得:x=1,
∴A的速度是1单位长度/秒,B的速度为2单位长度/秒,
∴A到达的位置为-4,B到达的位置是12,在数轴上的位置如图:
![]()
答:A的速度为1单位长度/秒;B的速度为2单位长度/秒;
(2)解:设y秒后,原点恰好在A、B的正中间,由题意,得:12-3y=y+4,y=2.
答:再过2秒时,原点恰好处在AB的中点
(3)解:设当C运动z秒后,C为AB的中点,由题意得:4+z+ ![]() z=12-3z-
z=12-3z-![]() z,
z,
解得:z= ![]() .
.
答:当C运动 ![]() 秒时,C为AB的中点.
秒时,C为AB的中点.
【解析】(1)设A的速度是x,则B的速度为3x, 根据4秒后,两点相距16个单位长度列出方程,求解即可;
(2)设y秒后,原点恰好在A、B的正中间,则A离原点的距离为y+4,B离原点的距离为12-3y ,根据A离原点的距离=B离原点的距离列出方程,求解即可;
(3)设当C运动z秒后,C为AB的中点,则A离C点的距离为4+z+ ![]() z ,B离C点的距离为12-3z-
z ,B离C点的距离为12-3z-![]() z, 根据A离C的距离=B离C的距离列出方程,求解即可.
z, 根据A离C的距离=B离C的距离列出方程,求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①,图②,图③都是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,在图③中已画出点A.按下列要求画图:
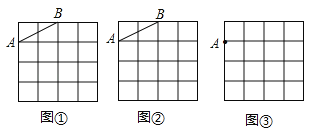
(1)在图①中,以格点为顶点,AB为一边画一个等腰三角形;
(2)在图②中,以格点为顶点,AB为一边画一个正方形;
(3)在图③中,以点A为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)如图(1),将一副直角三角板的直角顶点C叠放在一起.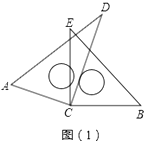
①填空:∠ACE∠BCD(选填“<”或“>”或“=”);
②若∠DCE=25°,求∠ACB的度数;
③猜想∠ACB与∠DCE的数量关系,并说明理由.
(2)若改变(1)中一个三角板的位置,如图(2)所示,则上述第③题的结论是否仍然成立?(不需要说明理由)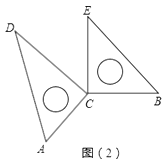
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是正方形ABCD对角线BD上一点,EM⊥BC,EN⊥CD垂足分别是求M、N

(1)求证:AE=MN;
(2)若AE=2,∠DAE=30°,求正方形的边长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,∠CBF=20°.
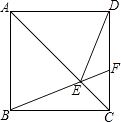
(1)∠ACB的大小=(度);
(2)求证:△ABE≌△ADE;
(3)∠AED的大小=(度). -
科目: 来源: 题型:
查看答案和解析>>【题目】在下午四点半钟的时候,时针和分针所夹的角度是( )
A. 30度 B. 45度 C. 60度 D. 75度
-
科目: 来源: 题型:
查看答案和解析>>【题目】某陶瓷商,为了促销决定卖一只茶壶,赠一只茶杯。某人共付款162元,买得茶壶茶杯共36只,已知每只茶壶15元,每只茶杯3元,问其中茶壶、茶杯各多少只?
相关试题

