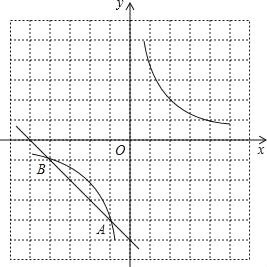
【题目】如图,在方格纸中(小正方形的边长为1),反比例函数的图象与直线的交点A、B均在格点上,根据所给的直角坐标系(O是坐标原点),解答下列问题:
(1)求这个反比例函数的解析式;
(2)若点C在已知的反比例函数的图象上,△ABC是以AB为底的等腰三角形,请写出点C的坐标.
参考答案:
【答案】(1)y=![]() (2)(2,2)或(﹣2,﹣2)
(2)(2,2)或(﹣2,﹣2)
【解析】
(1)设这个反比例函数的解析式是y=![]() ,把A点的坐标代入,即可求出答案;
,把A点的坐标代入,即可求出答案;
(2)设C点的坐标为(x,![]() ),根据两点之间距离公式和AC=BC得出方程,求出x即可.
),根据两点之间距离公式和AC=BC得出方程,求出x即可.
(1)设这个反比例函数的解析式是y=![]() ,
,
由图象可知:点A的坐标为(﹣1,﹣4),
代入得:k=4,
所以这个反比例函数的解析式是y=![]() ;
;
(2)设C点的坐标为(x,![]() ),
),
∵A(﹣1,﹣4),B(﹣4,﹣1),AC=BC,
∴根据两点之间距离公式得:(﹣1﹣x)2+(﹣4﹣![]() )2=(﹣4﹣x)2+(﹣1﹣
)2=(﹣4﹣x)2+(﹣1﹣![]() )2,
)2,
解得:x=±2,
当x=2时,![]() =2;
=2;
当x=﹣2时,![]() =﹣2,
=﹣2,
所以点C的坐标为(2,2)或(﹣2,﹣2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到(a+b)2=a2+2ab+b2,基于此,请解答下列问题:
(1)根据如图2,写出一个代数恒等式: .
(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,则a2+b2+c2= .
(3)小明同学用如图3中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片拼出一个面积为(2a+b)(a+2b)长方形,则x+y+z= .
(4)两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成如图4.请你根据如图中图形的关系,写出一个代数恒等式,并写出推导过程.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE.正确的是( )
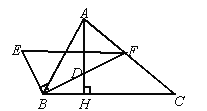
A. ①②③④ B. ①② C. ①③④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格;

(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于
 ,求m的值.
,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣4,n),B(4﹣n,﹣4)是直线y=kx+b和双曲线y=
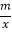 的两个交点.
的两个交点.(1)求两个函数的表达式;
(2)观察图象,直接写出不等式kx+b﹣
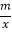 ≥0的解集.
≥0的解集.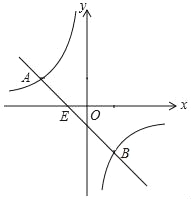
-
科目: 来源: 题型:
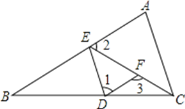
查看答案和解析>>【题目】如图,已知:∠A=∠1,∠2+∠3=180°,∠BDE=65°,
(1)AB与DF平行吗?说明理由;
(2)求∠ACB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,以AC为直径的⊙O与边AB,BC分别交于点D,E.过E的直线与⊙O相切,与AC的延长线交于点G,与AB交于点F.
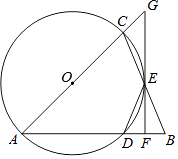
(1)求证:△BDE为等腰三角形;
(2)求证:GF⊥AB;
(3)若⊙O半径为3,DF=1,求CG的长.
相关试题

