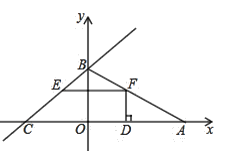
【题目】如图,已知直线![]() 与坐标轴交于
与坐标轴交于![]() ,
,![]() 两点,点
两点,点![]() 是
是![]() 轴正半轴上一点,并且
轴正半轴上一点,并且![]() ,点
,点![]() 是线段
是线段![]() 上一动点(不与端点重合),过点
上一动点(不与端点重合),过点![]() 作
作![]() 轴,交
轴,交![]() 于
于![]() .
.
(1)求![]() 所在直线的解析式;
所在直线的解析式;
(2)若![]() 轴于
轴于![]() ,且点
,且点![]() 的坐标为
的坐标为![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 与
与![]() 的长;
的长;
(3)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 为等腰直角三角形?若存在,请直接写出点
为等腰直角三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)存在满足条件的点
;(3)存在满足条件的点![]() ,其坐标为
,其坐标为![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() .
.
【解析】
(1)由直线![]() 可求得
可求得![]() 、
、![]() 坐标,再结合
坐标,再结合![]() ,则可求得
,则可求得![]() 点坐标,利用待定系数法可求得直线
点坐标,利用待定系数法可求得直线![]() 的解析式;
的解析式;
(2)根据直线![]() 解析式可求得
解析式可求得![]() 点的纵坐标,即可表示出
点的纵坐标,即可表示出![]() 的长,由
的长,由![]() 轴则可得出
轴则可得出![]() 点纵坐标,代入直线
点纵坐标,代入直线![]() 解析式可求得
解析式可求得![]() 点横坐标,从而可表示出
点横坐标,从而可表示出![]() 的长;
的长;
(3)设![]() ,当
,当![]() 时,则有
时,则有![]() ,则可得到关于x的方程,可求得
,则可得到关于x的方程,可求得![]() 点坐标;当
点坐标;当![]() 时,则有
时,则有![]() ,可求得
,可求得![]() 点坐标;当
点坐标;当![]() 时,过
时,过![]() 作
作![]() ,由等腰直角三角形的性质可知
,由等腰直角三角形的性质可知![]() ,可求得
,可求得![]() 点坐标,从而可求得
点坐标,从而可求得![]() 点坐标.
点坐标.
解:
(1)在![]() 中,令
中,令![]() 可得
可得![]() ,令
,令![]() 可求得
可求得![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
![]()
![]() ,解得
,解得 ,
,
![]() 直线
直线![]() 解析式为
解析式为![]() ;
;
(2)![]() 轴,且
轴,且![]() ,
,
![]() 点横坐标为
点横坐标为![]() ,
,
在![]() 中,令
中,令![]() ,可得
,可得![]() ,
,
![]() ,
,
![]() 轴,
轴,
![]() 点纵坐标为
点纵坐标为![]() ,
,
在![]() 中,令
中,令![]() ,可得
,可得![]() ,解得
,解得![]() ,
,
![]() 在线段
在线段![]() 上,
上,
![]()
![]() ;
;
(3)假设存在满足条件的点![]() ,设其坐标为
,设其坐标为![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() 有
有![]() 、
、![]() 和
和![]() 三种情况,
三种情况,
①当![]() 时,则有
时,则有![]() ,
,
由(2)可得![]() ,
,![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() ,
,![]() ;
;
②当![]() 时,则有
时,则有![]() ,
,
在![]() 中,令
中,令![]() 可得
可得![]() ,
,
![]() ,
,
在![]() 中,令
中,令![]() ,可得
,可得![]() ,解得
,解得![]() ,
,
![]() ,
,
![]()
![]() ,解得
,解得![]() ,
,
![]() ,
,![]() ;
;
③当![]() 时,如图,过
时,如图,过![]() 作
作![]() 于点
于点![]() ,则
,则![]() ,
,
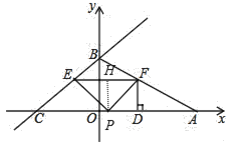
由(2)可知![]() ,
,![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ;
;
综上可知存在满足条件的点![]() ,其坐标为
,其坐标为![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(-2,2),B(8,12)在抛物线y=ax2+bx上.
(1)求抛物线的解析式;
(2)如图1,点F的坐标为(0,m)(m>4),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H,设抛物线与x轴的正半轴交于点E,连接FH、AE,求
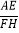 之值(用含m的代数式表示);
之值(用含m的代数式表示);(3)如图2,直线AB分别交x轴、y轴于C、D两点,点P从点C出发,沿射线CD方向匀速运动,速度为每秒
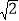 个单位长度,同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度,点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=3PM,求t的值.
个单位长度,同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度,点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=3PM,求t的值.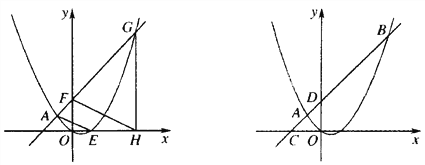
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,点
中,点 是
是 边上的一个动点,过点
边上的一个动点,过点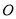 作直线
作直线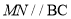 ,设
,设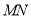 交
交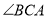 的角平分线于点
的角平分线于点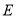 ,交
,交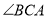 的外角平分线于点
的外角平分线于点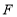 .
.(1)求证:
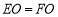 ;
;(2)当点
 运动到何处时,四边形
运动到何处时,四边形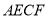 是矩形?并证明你的结论.
是矩形?并证明你的结论.(3)当点
 运动到何处,且
运动到何处,且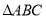 满足什么条件时,四边形
满足什么条件时,四边形 是正方形?并说明理由.
是正方形?并说明理由.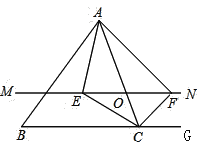
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 为线段
为线段 上一点,点
上一点,点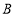 为
为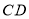 的中点,且
的中点,且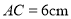 ,
,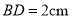 .
.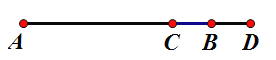
(1)图中共有______条线段,分别是______;
(2)求线段
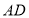 的长;
的长;(3)若点
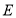 在直线
在直线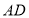 上,且
上,且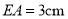 ,求线段
,求线段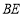 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面直角坐标系
 如图
如图 ,直线
,直线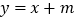 的经过点
的经过点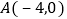 和点
和点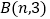 .
.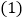 求m、n的值;
求m、n的值;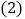 如果抛物线
如果抛物线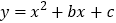 经过点A、B,该抛物线的顶点为点P,求
经过点A、B,该抛物线的顶点为点P,求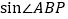 的值;
的值;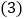 设点Q在直线
设点Q在直线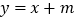 上,且在第一象限内,直线
上,且在第一象限内,直线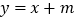 与y轴的交点为点D,如果
与y轴的交点为点D,如果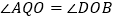 ,求点Q的坐标.
,求点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
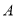 在反比例函数,
在反比例函数,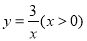 的图像上,点
的图像上,点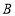 在反比例函数
在反比例函数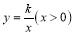 的图像上,
的图像上,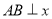 轴于点
轴于点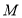 .且
.且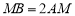 ,则
,则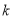 的值为( )
的值为( )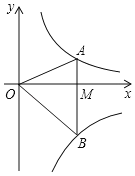
A.-3B.-6C.2D.6
-
科目: 来源: 题型:
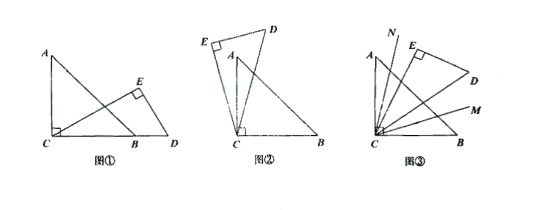
查看答案和解析>>【题目】如图,将一个直角三角板中30°的锐角顶点与另一个直角三角板的直角顶点叠放一起.(注:∠ACB与∠DEC是直角,∠A=45°,∠DEC=30°).
(1)如图①,若点C、B、D在一条直线上,求∠ACE的度数;
(2)如图②,将直角三角板CDE绕点c逆时针方向转动到某个位置,若恰好平分∠DCE,求∠BCD的度数;
(3)如图③若∠DEC始终在∠ACB的内部,分别作射线CM平分∠BCD,射线CN平分∠ACE.如果三角板DCE在∠ACB内绕点C任意转动,∠MCN的度数是否发生变化?如果不变,求出它的度数,如果变化,说明理由。
相关试题

