【题目】已知点A(-2,2),B(8,12)在抛物线y=ax2+bx上.
(1)求抛物线的解析式;
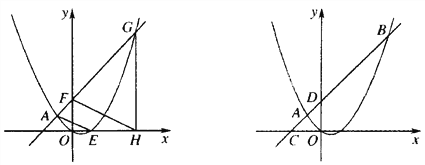
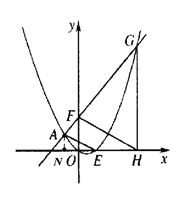
(2)如图1,点F的坐标为(0,m)(m>4),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H,设抛物线与x轴的正半轴交于点E,连接FH、AE,求![]() 之值(用含m的代数式表示);
之值(用含m的代数式表示);
(3)如图2,直线AB分别交x轴、y轴于C、D两点,点P从点C出发,沿射线CD方向匀速运动,速度为每秒![]() 个单位长度,同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度,点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=3PM,求t的值.
个单位长度,同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度,点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=3PM,求t的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ,
,![]()
【解析】分析:(1)、根据点A、B的坐标利用待定系数法,即可求出抛物线的解析式;(2)、根据点A、F的坐标利用待定系数法,可求出直线AF的解析式,联立直线AF和抛物线的解析式成方程组,通过解方程组可求出点G的坐标,过A作AN⊥x轴于点N得出点N的坐标,根据方程求出x的值得出答案;(3)、根据点A、B的坐标利用待定系数法,可求出直线AB的解析式,进而可找出点P、Q的坐标,分点M在线段PQ上以及点M在线段QP的延长线上两种情况考虑,借助相似三角形的性质可得出点M的坐标,再利用二次函数图象上点的坐标特征可得出关于t的一元二次方程,解之即可得出结论.
详解:解:(1)、点A(-2,2),B(8,12)在抛物线y=ax2+bx上,∴![]() ∴
∴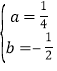 ,∴
,∴![]() ;
;
(2)、设直线AF的解析式为y=kx+m, ∵A(-2,2)在AF上,∴2=-2k+m,k=![]() (m-2),
(m-2),
∴直线y=kx+m可化为![]() , 则
, 则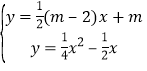
∴x2-2(m-1)x-4m=0, ∴(x+2)(x-2m)=0,∴x=-2或x=2m, ∴G的横坐标为2m,
∴OH=2m,∵OF=m,∴FH=![]() ,过A作AN⊥x轴于点N,则N(-2,0),
,过A作AN⊥x轴于点N,则N(-2,0),
令![]() ,∴x=0或x=2, ∴OE=2,NE=4 ∴AE=
,∴x=0或x=2, ∴OE=2,NE=4 ∴AE=![]() ,∴
,∴![]() ;
;
(3)、由题意A(-2,2),B(8,12),直线AB的解析式为:y=x+4,∠BCO=45°,
直线AB与x轴交点为C(-4,0),设P(t-4,t),则Q(t,0),设M(![]() ,
,![]() )
)
由QM=3PM可得,则|t-![]() |=3|
|=3|![]() -t+4|,
-t+4|,
(ⅰ)当t-![]() =3(
=3(![]() -t+4)即
-t+4)即![]() =t-3,直线PQ的解析式为tx+4y-t2=0,
=t-3,直线PQ的解析式为tx+4y-t2=0,
∴![]() =
=![]() ,∴M(t-3,
,∴M(t-3,![]() ),代入
),代入![]() 即
即![]() ,
,
∴t2-11t+15=0,∴![]() ,即:
,即:![]() ,
,![]() ;
;
(ⅱ)当![]() -t=3(
-t=3(![]() -t+4)即
-t+4)即![]() =t-6,∴
=t-6,∴![]() ,∴
,∴![]() ,
,
代入![]() 即
即![]() ,∴t2-20t+48=0,
,∴t2-20t+48=0,
∴![]() , 即:
, 即:![]() ,
,![]() ;
;
综上所述,所求t为:![]() ,
,![]() ,
,![]() ,
,![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.邮箱中剩余油量Q(L)与行驶时间t(h)之间的函数关系如图所示.
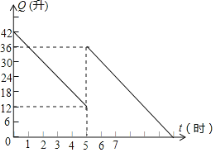
(1)汽车行驶 h后加油,加油量为 L;
(2)求加油前油箱剩余油量Q与行驶时间t之间的函数关系式;
(3)如果加油站离目的地还有200km,车速为40km/h,请直接写出汽车到达目的地时,油箱中还有多少汽油?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市在城中村改造中,需要种植
 、
、 两种不同的树苗共
两种不同的树苗共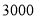 棵,经招标,承包商以
棵,经招标,承包商以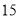 万元的报价中标承包了这项工程,根据调查及相关资料表明,
万元的报价中标承包了这项工程,根据调查及相关资料表明, 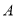 、
、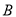 两种树苗的成本价及成活率如表:
两种树苗的成本价及成活率如表:品种
购买价(元/棵)
成活率

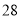
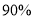


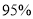
设种植
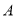 种树苗
种树苗 棵,承包商获得的利润为
棵,承包商获得的利润为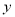 元.
元.(
 )求
)求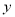 与
与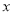 之间的函数关系式.
之间的函数关系式.(
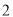 )政府要求栽植这批树苗的成活率不低于
)政府要求栽植这批树苗的成活率不低于
,承包商应如何选种树苗才能获得最大利润?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图 .在数轴.上有
 两个点(点
两个点(点 在点
在点 的左侧) ,
的左侧) , 

(1)如果点
 表示的数是
表示的数是 ,那么,
,那么,①点
 表示的数是_______.
表示的数是_______.②如果点
 从点
从点 出发,沿数轴正方向运动,速度是每秒3个单位长度,运动秒后,点
出发,沿数轴正方向运动,速度是每秒3个单位长度,运动秒后,点 表示的数是_______.( 用含
表示的数是_______.( 用含 的代数式表示) ; 经过________秒 ,
的代数式表示) ; 经过________秒 ,  .
.(2)如果点
 表示的数是
表示的数是 ,将数轴的负半轴绕原点
,将数轴的负半轴绕原点 顺时针旋转60° ,得到
顺时针旋转60° ,得到 ,如图2所示,射线
,如图2所示,射线 从
从 出发绕点
出发绕点 顺时针旋转,速度是每秒15° ,同时,射线
顺时针旋转,速度是每秒15° ,同时,射线 从
从 出发绕点
出发绕点 逆时针旋转,速度是每秒5° .设运动时间为
逆时针旋转,速度是每秒5° .设运动时间为 秒,当
秒,当 秒时,
秒时,  停止运动.
停止运动.①当
 为________秒时,
为________秒时, 与
与 重合.
重合.②当
 时,
时, 的值是________.
的值是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
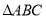 中,点
中,点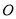 是
是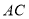 边上的一个动点,过点
边上的一个动点,过点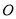 作直线
作直线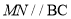 ,设
,设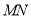 交
交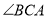 的角平分线于点
的角平分线于点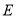 ,交
,交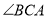 的外角平分线于点
的外角平分线于点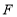 .
.(1)求证:
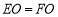 ;
;(2)当点
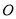 运动到何处时,四边形
运动到何处时,四边形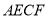 是矩形?并证明你的结论.
是矩形?并证明你的结论.(3)当点
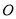 运动到何处,且
运动到何处,且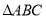 满足什么条件时,四边形
满足什么条件时,四边形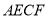 是正方形?并说明理由.
是正方形?并说明理由.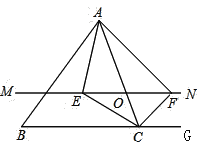
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
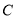 为线段
为线段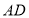 上一点,点
上一点,点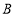 为
为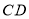 的中点,且
的中点,且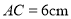 ,
,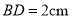 .
.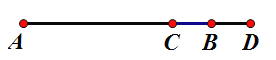
(1)图中共有______条线段,分别是______;
(2)求线段
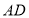 的长;
的长;(3)若点
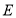 在直线
在直线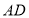 上,且
上,且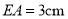 ,求线段
,求线段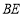 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
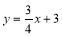 与坐标轴交于
与坐标轴交于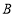 ,
,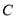 两点,点
两点,点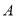 是
是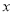 轴正半轴上一点,并且
轴正半轴上一点,并且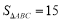 ,点
,点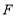 是线段
是线段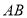 上一动点(不与端点重合),过点
上一动点(不与端点重合),过点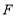 作
作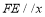 轴,交
轴,交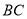 于
于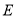 .
.(1)求
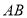 所在直线的解析式;
所在直线的解析式;(2)若
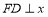 轴于
轴于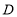 ,且点
,且点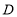 的坐标为
的坐标为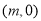 ,请用含
,请用含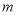 的代数式表示
的代数式表示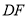 与
与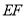 的长;
的长;(3)在
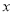 轴上是否存在一点
轴上是否存在一点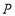 ,使得
,使得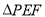 为等腰直角三角形?若存在,请直接写出点
为等腰直角三角形?若存在,请直接写出点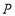 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
相关试题

