【题目】如图,Rt△OAB的直角边OA在x轴上,顶点B的坐标为(6,8),直线CD交AB于点D(6,3),交x轴于点C(12,0).
(1)求直线CD的函数表达式;
(2)动点P在x轴上从点(﹣10,0)出发,以每秒1个单位的速度向x轴正方向运动,过点P作直线l垂直于x轴,设运动时间为t.
①点P在运动过程中,是否存在某个位置,使得∠PDA=∠B?若存在,请求出点P的坐标;若不存在,请说明理由;
②请探索当t为何值时,在直线l上存在点M,在直线CD上存在点Q,使得以OB为一边,O,B,M,Q为顶点的四边形为菱形,并求出此时t的值.

参考答案:
【答案】(1)直线CD的解析式为y=﹣![]() x+6;(2)①满足条件的点P坐标为(
x+6;(2)①满足条件的点P坐标为(![]() ,0)或(
,0)或(![]() ,0).②满足条件的t的值为
,0).②满足条件的t的值为![]() 或
或![]() .
.
【解析】
(1)利用待定系数法即可解决问题;
(2)①如图1中,作DP∥OB,则∠PDA=∠B.利用平行线分线段成比例定理,计算即可,再根据对称性求出P′;
②分两种情形分别求解即可解决问题:如图2中,当OP=OB=10时,作PQ∥OB交CD于Q.如图3中,当OQ=OB时,设Q(m,﹣![]() m+6),构建方程求出点Q坐标即可解决问题;
m+6),构建方程求出点Q坐标即可解决问题;
(1)设直线CD的解析式为y=kx+b,则有
![]() ,
,
解得 ,
,
∴直线CD的解析式为y=﹣![]() x+6.
x+6.
(2)①如图1中,作DP∥OB,则∠PDA=∠B.
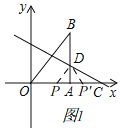
∵DP∥OB,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴OP=6﹣![]() ,
,
∴P(![]() ,0),
,0),
根据对称性可知,当AP=AP′时,P′(![]() ,0),
,0),
∴满足条件的点P坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).
②如图2中,当OP=OB=10时,作PQ∥OB交CD于Q.
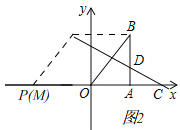
∵直线OB的解析式为y=![]() x,
x,
∴直线PQ的解析式为y=![]() x+
x+![]() ,
,
由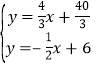 ,
,
解得![]() ,
,
∴Q(﹣4,8),
∴PQ=![]() =10,
=10,
∴PQ=OB.
∵PQ∥OB,
∴四边形OBQP是平行四边形.
∵OB=OP,
∴四边形OBQP是菱形,此时点M与的Q重合,满足条件,t=0.
如图3中,当OQ=OB时,设Q(m,﹣![]() m+6),
m+6),
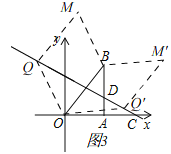
则有m2+(﹣![]() m+6)2=102,解得m=
m+6)2=102,解得m=![]() ,
,
∴点Q 的横坐标为![]() 或
或![]() ,
,
设点M的横坐标为a,则有:![]() 或
或![]() ,
,
∴a=![]() 或
或![]() ,
,
∴满足条件的t的值为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间接到一批限期(可以提前)完成的零件加工任务.如果每天加工150个,则恰好按期完成;如果每天加工200个,则可比原计划提前5天完成.
(1)求这批零件的个数;
(2)车间按每天加工200个零件的速度加工了
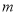 个零件后,提高了加工速度,每天加工250个零件,结果比原计划提前6天完成了生产任务,求
个零件后,提高了加工速度,每天加工250个零件,结果比原计划提前6天完成了生产任务,求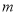 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 是直线
是直线 上一点,
上一点, ,
, 是
是 的平分线.
的平分线.(1)当点
 ,
, 在直线
在直线 的同侧,且
的同侧,且 在
在 的内部时(如图1所示 ), 设
的内部时(如图1所示 ), 设 ,求
,求 的大小;
的大小;(2)当点
 与点
与点 在直线
在直线 的两旁(如图2所示),(1)中的结论是否仍然成立?请给出你的结论,并说明理由;
的两旁(如图2所示),(1)中的结论是否仍然成立?请给出你的结论,并说明理由;(3)将图2 中的射线
 绕点
绕点 顺时针旋转
顺时针旋转 ,得到射线
,得到射线 ,设
,设 ,若
,若 ,则
,则 的度数是 (用含
的度数是 (用含 的式子表示)
的式子表示)

-
科目: 来源: 题型:
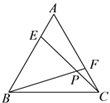
查看答案和解析>>【题目】如图,点E、点F分别是等边△ABC的边AB、AC上的点,且BE=AF,CE、BF 相交于点P,则∠BPC的大小为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列四项调查中,方式正确的是


A. 了解本市中学生每天学习所用的时间,采用全面调查的方式
B. 为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式
C. 了解某市每天的流动人口数,采用全面调查的方式
D. 了解全市中学生的视力情况,采用抽样调查的方式
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC,直线,MN经过点C,且AD⊥MN于点D,BE⊥MN于点E。

(1)当直线MN绕点C旋转到如图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到如图2的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到如图3的位置时,线段DE、AD、BE之间又有什么样的数量关系?请你写出这个数量关系,并证明
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则A2017的坐标为( )
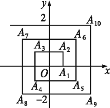
A.(505,504)B.(505,-504)C.(-504,504)D.(-504,-504)
相关试题

