【题目】一架方梯长25米,如图,斜靠在一面墙上,梯子底端离墙7米.

(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
(3)当梯子的顶端下滑的距离与梯子的底端水平滑动的距离相等时,这时梯子的顶端距地面有多高?
参考答案:
【答案】(1)梯子距离地面的高度为24米;(2)梯子的底端在水平方向滑动了8米;(3)梯子顶端距离地面的高度为7米.
【解析】
(1)根据勾股定理即可求出答案;(2)由(1)可知梯子的顶端距地面有多高,从而可知梯子顶端下滑4米后距地面的距离,根据勾股定理即可求出梯子底部距离墙面的距离,从而得出答案;(3)设梯子的顶端下滑的距离与梯子的底端水平滑动的距离相等为x,根据勾股定理列式解答即可。
解:(1)根据勾股定理:梯子距离地面的高度为:![]() 米;
米;
(2)梯子下滑了4米,即梯子距离地面的高度为(24﹣4)=20米,
根据勾股定理:![]() ,解得A'B=8米.即下端滑行了8米.
,解得A'B=8米.即下端滑行了8米.
(3)设梯子的顶端下滑的距离与梯子的底端水平滑动的距离相等为x,
根据题意,![]() ,解得,x=17米,
,解得,x=17米,
即梯子顶端距离地面的高度为(24﹣17)=7米.
答:(1)梯子距离地面的高度为24米;(2)梯子的底端在水平方向滑动了8米;
(3)梯子顶端距离地面的高度为7米
-
科目: 来源: 题型:
查看答案和解析>>【题目】在水果销售旺季,某水果店购进一优质水果,进价为 20 元/千克,售价不低于 20 元/千克,且不超过 32 元/千克,根据销售情况,发现该水果一天的销售量 y(千克)与该天的售价 x(元/千克)满足如下表所示的一次函数关系.
销售量 y(千克)
…
34.8
32
29.6
28
…
售价 x(元/千克)
…
22.6
24
25.2
26
…
(1)某天这种水果的售价为 23.5 元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利 150 元,那么该天水果的售价为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小方格都是边长为1个单位的正方形,若学校位置坐标为A(2,1),图书馆位置坐标为B(﹣1,﹣2),解答以下问题:
(1)在图中标出平面直角坐标系的原点,并建立直角坐标系;
(2)若体育馆位置坐标为C(1,﹣3),请在坐标系中标出体育馆的位置;
(3)顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
小明遇到一个问题:在
 中,
中, ,
,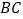 ,
, 三边的长分别为
三边的长分别为 、
、 、
、 ,求
,求 的面积.
的面积.小明是这样解决问题的:如图①所示,先画一个正方形网格(每个小正方形的边长为
 ),再在网格中画出格点
),再在网格中画出格点 (即
(即 三个顶点都在小正方形的顶点处),从而借助网格就能计算出
三个顶点都在小正方形的顶点处),从而借助网格就能计算出 的面积.他把这种解决问题的方法称为构图法.
的面积.他把这种解决问题的方法称为构图法.参考小明解决问题的方法,完成下列问题:
(
 )图
)图 是一个
是一个 的正方形网格(每个小正方形的边长为
的正方形网格(每个小正方形的边长为 ) .
) .①利用构图法在答卷的图
 中画出三边长分别为
中画出三边长分别为 、
、 、
、 的格点
的格点 .
. ②计算①中
 的面积为__________.(直接写出答案)
的面积为__________.(直接写出答案)(
 )如图
)如图 ,已知
,已知 ,以
,以 ,
, 为边向外作正方形
为边向外作正方形 ,
, ,连接
,连接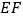 .
.①判断
 与
与 面积之间的关系,并说明理由.
面积之间的关系,并说明理由.②若
 ,
, ,
, ,直接写出六边形
,直接写出六边形 的面积为__________.
的面积为__________.


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:边长为2的正方形OABC在平面直角坐标系中位于x轴上方,OA与x轴的正半轴的夹角为60°,则B点的坐标为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知O为坐标原点,长方形ABCD(点A与坐标原点重合)的顶点D、B分别在x轴、y轴上,且点C的坐标为(-4,8),连接BD,将△ABD沿直线BD翻折至△A
 BD,交CD于点E.
BD,交CD于点E.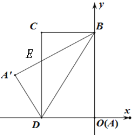
(1)求S△BED的面积;
(2)求点A
 坐标.
坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.
△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)求证:△ACB∽△DCE;(2)求证:EF⊥AB.

相关试题

