【题目】如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、M两点,若点M的坐标是(-4,-2),则点N的坐标为( )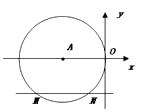
A.(-1,-2)
B.(1,2)
C.(-1.5,-2)
D.(1.5,-2)
参考答案:
【答案】A
【解析】如图:分别过点M、N作x轴的垂线,过点A作AB⊥MN,连接AN,
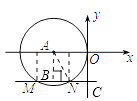
设⊙A的半径为r.
则AN=OA=r,AB=2,
∵AB⊥MN,∴BM=BN,
∴BN=BM=4-r;
则在Rt△ABN中,根据勾股定理,得AB2+BN2=AN2,
即:22+(4-r)2=r2,解得r=2.5,
所以BM=BN=4-2.5=1.5,则N到y轴的距离为2.5-1.5=1,
又∵点N在第三象限,∴N的坐标为(-1,-2)
所以答案是:A.
【考点精析】关于本题考查的勾股定理的概念和垂径定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,D为△ABC所在平面内的一点,过D作DE∥AB,DF∥AC分别交直线AC,直线AB于点E,F.
(1)如图1,当点D在线段BC上时,通过观察分析线段DE、DF、AB之间的数量关系,并说明理由;
(2)如图2,当点D在直线BC上,其他条件不变时,试猜想线段DE、DF、AB之间的数量关系(请直接写出等式,不需证明);
(3)如图3,当点D是△ABC内一点,过D作DE∥AB,DF∥AC分别交直线AC,直线AB和直线BC于E、F和G. 试猜想线段DE、DF、DG与AB之间的数量关系(请直接写出等式,不需证明).

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
 ÷
÷ -
- ×
×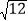 +
+ ; (2)
; (2) -
- -(
-(
 -2
-2 );
);(3)(2-
 )2017×(2+
)2017×(2+ )2016-2
)2016-2 -(-
-(- )0 (4)(a+2
)0 (4)(a+2 +b)÷(
+b)÷( +
+ )-(
)-( -
- ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】若两个扇形满足弧长的比等于它们半径的比,则这称这两个扇形相似。如图,如果扇形AOB与扇形
 是相似扇形,且半径
是相似扇形,且半径  (
(  为不等于0的常数)那么下面四个结论:①∠AOB=∠ A1O1B1
为不等于0的常数)那么下面四个结论:①∠AOB=∠ A1O1B1  ;②△AOB∽△
;②△AOB∽△  A1O1B1 ;③
A1O1B1 ;③  A1B1 =k;④扇形AOB与扇形 A1O1B1
A1B1 =k;④扇形AOB与扇形 A1O1B1  的面积之比为
的面积之比为  。成立的个数为:( )
。成立的个数为:( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】解决问题:
一辆货车从超市出发,向东走了3千米到达小彬家,继续走2.5千米到达小颖家,然后向西走了10千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家,小彬家,小颖家的位置.
(2)小明家距小彬家多远?
(3)货车一共行驶了多少千米?
(4)货车每千米耗油0.2升,这次共耗油多少升?
相关试题

