【题目】如图,已知△ABC中,AB=AC,D为△ABC所在平面内的一点,过D作DE∥AB,DF∥AC分别交直线AC,直线AB于点E,F.
(1)如图1,当点D在线段BC上时,通过观察分析线段DE、DF、AB之间的数量关系,并说明理由;
(2)如图2,当点D在直线BC上,其他条件不变时,试猜想线段DE、DF、AB之间的数量关系(请直接写出等式,不需证明);
(3)如图3,当点D是△ABC内一点,过D作DE∥AB,DF∥AC分别交直线AC,直线AB和直线BC于E、F和G. 试猜想线段DE、DF、DG与AB之间的数量关系(请直接写出等式,不需证明).

参考答案:
【答案】(1)DE+DF=AB.理由见解析; (2) ①当点D在CB的延长线上时, AB=DE-DF;②当点D在线段BC上时,AB=DE+DF;③当点D在BC的延长线上时, AB=DF-DE.(3)AB=DE+DG+DF.
【解析】
(1)如图1,先根据两组对边分别平行的四边形是平行四边形得出四边形AEDF是平行四边形,则DE=AF.再根据平行线及等腰三角形的性质得出∠FDB=∠B,由等角对等边得到DF=FB,从而证明DE+DF=AF+FB=AB;
(2)当点D在直线BC上时,分三种情况:
①当点D在BC的反向延长线上时,如图4,先证明四边形AEDF是平行四边形,则DE=AF,再证明∠FDB=∠FBD,由等角对等边得到DF=FB,从而证明AB=AF-BF=DE-DF;
②当点D在线段BC上时,如图1,AB=DE+DF;
③当点D在BC的延长线上时,如图5,先证明四边形AEDF是平行四边形,则DF=AE,再证明∠CDE=∠DCE,由等角对等边得到CE=DE,再证明从而证明AB=AC=AE-CE=DF-DE;
(3)如图3,先证明四边形AEDF是平行四边形,则DF=AE,再证明∠EGC=∠C,由等角对等边得到DE+DG=CE,从而证明AB=AC=EC+AE=DE+DG+DF.
(1)DE+DF=AB. 理由如下:
如图1,∵DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形,
∴DE=AF.
∵DF∥AC,
∴∠FDB=∠C,
∵AB=AC,
∴∠C=∠B,
∴∠FDB=∠B,
∴DF=FB,
∴DE+DF=AF+FB=AB;
(2)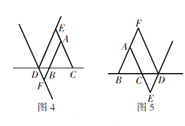
①当点D在BC的反向延长线上时,如图4,AB=DE-DF;
∵DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形,
∴DE=AF.
∴∠FDB=∠BCA,
∵AB=AC,
∴∠BCA =∠B,
∴∠FDB=∠B=∠DBF,
∴DF=FB,
∴AB=AF-BF=DE-DF;;
②当点D在线段BC上时,同题(1),AB=DE+DF;
③当点D在BC的延长线上时,如图5,AB=DF-DE;
∵DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形,
∴DF=AE.
∴∠CDE=∠B,
∵AB=AC,
∴∠BCA =∠B=∠DCE ,
∴∠CDE=∠DCE,
∴CE=DE,
∴AB=AC=AE-CE=DF-DE;;
(3)AB=DE+DG+DF.
∵DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形,
∴DF=AE,
∵DE∥AB,
∴∠EGC=∠B,
∵AB=AC,
∴∠C=∠B,
∴∠C=∠EGC,
∴EG=EC,即DE+DG=CE,
∴AB=AC=EC+AE=DE+DG+DF.
故答案为:(1)DE+DF=AB. 理由见解析;(2)①当点D在BC的反向延长线上时,如图4见解析,AB=DE-DF;②当点D在线段BC上时,同题(1),AB=DE+DF;③当点D在BC的延长线上时,如图5见解析,AB=DF-DE;(3)AB=DE+DG+DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,BC⊥CD,E是AD的中点,连结BE并延长交CD的延长线于点F.
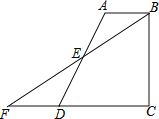
(1)请连结AF、BD,试判断四边形ABDF是何种特殊四边形,并说明理由.
(2)若AB=4,BC=5,CD=6,求△BCF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下面给出的数轴,解答下面的问题:
(1)请你根据图中A、B两点的位置,分别写出它们所表示的有理数A:_____B:_____.
(2)观察数轴,与点A的距离为4的点表示的数是:_____.
(3)若将数轴折叠,使得A点与﹣2表示的点重合,则B点与数_____表示的点重合.
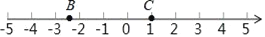
-
科目: 来源: 题型:
查看答案和解析>>【题目】请根据图示的对话解答下列问题.

求:(1)a,b的值;
(2)8﹣a+b﹣c的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
 ÷
÷ -
- ×
×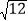 +
+ ; (2)
; (2) -
- -(
-(
 -2
-2 );
);(3)(2-
 )2017×(2+
)2017×(2+ )2016-2
)2016-2 -(-
-(- )0 (4)(a+2
)0 (4)(a+2 +b)÷(
+b)÷( +
+ )-(
)-( -
- ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、M两点,若点M的坐标是(-4,-2),则点N的坐标为( )
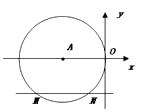
A.(-1,-2)
B.(1,2)
C.(-1.5,-2)
D.(1.5,-2)
相关试题

