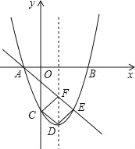
【题目】如图,二次函数y=ax2+bx+c的图象与x轴相交于点A(﹣1,0),B(3,0),与y轴相交于点C(0,﹣3).
(1)求此二次函数的解析式.
(2)若抛物线的顶点为D,点E在抛物线上,且与点C关于抛物线的对称轴对称,直线AE交对称轴于点F,试判断四边形CDEF的形状,并说明理由.
(3)若点M在x轴上,点P在抛物线上,是否存在以A,E,M,P为顶点且以AE为一边的平行四边形?若存在,请直接写出所有满足要求的点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)抛物线的解析式为y=x2﹣2x﹣3.
(2)四边形EFCD是正方形;
(3)当P点坐标为(1+![]() ,2)或(1﹣
,2)或(1﹣![]() ,2)或(0,﹣2)时,存在以A,E,M,P为顶点且以AE为一边的平行四边形.
,2)或(0,﹣2)时,存在以A,E,M,P为顶点且以AE为一边的平行四边形.
【解析】
试题分析:(1)利用待定系数法即可解决问题.
(2)结论四边形EFCD是正方形.如图1中,连接CE与DF交于点K.求出E、F、D、C四点坐标,只要证明DF⊥CE,DF=CE,KC=KE,KF=KD即可证明.
(3)如图2中,存在以A,E,M,P为顶点且以AE为一边的平行四边形.根据点P的纵坐标为2或﹣2,即可解决问题.
试题解析:(1)把A(﹣1,0),B(3,0),C(0,﹣3)代入y=ax2+bx+c得 ,
,
解得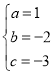 ,∴抛物线的解析式为y=x2﹣2x﹣3.
,∴抛物线的解析式为y=x2﹣2x﹣3.
(2)结论四边形EFCD是正方形.
理由:如图1中,连接CE与DF交于点K.
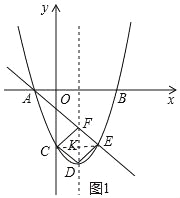
∵y=(x﹣1)2﹣4,∴顶点D(1,4),∵C、E关于对称轴对称,C(0,﹣3),
∴E(2,﹣3),∵A(﹣1,0),设直线AE的解析式为y=kx+b,
∴![]() ,解得
,解得![]() ,
,
∴直线AE的解析式为y=﹣x﹣1.
∴F(1,﹣2),
∴CK=EK=1,FK=DK=1,
∴四边形EFCD是平行四边形,
又∵CE⊥DF,CE=DF,
∴四边形EFCD是正方形.
(3)如图2中,存在以A,E,M,P为顶点且以AE为一边的平行四边形.

由题意点P的纵坐标为2或﹣2,
当y=2时,x2﹣2x﹣3=2,解得x=1±![]() ,
,
可得P1(1+![]() ,2),P2(1-
,2),P2(1-![]() ,2),
,2),
当y=﹣2时,x=0,可得P3(0,﹣2),
综上所述当P点坐标为(1+ ![]() ,2)或(1﹣
,2)或(1﹣![]() ,2)或(0,﹣2)时,存在以A,E,M,P为顶点且以AE为一边的平行四边形.
,2)或(0,﹣2)时,存在以A,E,M,P为顶点且以AE为一边的平行四边形.
-
科目: 来源: 题型:
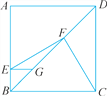
查看答案和解析>>【题目】如图,在正方形ABCD中,点E,G分别在边AB,对角线BD上,EG∥AD,F为GD的中点,连结FC,请利用勾股定理的逆定理,证明EF⊥FC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】安宁市的一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,若经粗加工后销售,每吨利润可达4500元;若经精加工后销售每吨获利7500元.当地一家农产品企业收购这种蔬菜140吨,该企业加工厂的生产能力是:如果对蔬菜进行粗加工,每天可以加工16吨,如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节条件限制,企业必须在15天的时间将这批蔬菜全部销售或加工完毕,企业研制了四种可行方案: 方案一:全部直接销售;
方案二:全部进行粗加工;
方案三:尽可能多地进行精加工,没有来得及进行精加工的直接销售;
方案四:将一部分进行精加工,其余的进行粗加工,并恰好15天完成.
请通过计算以上四个方案的利润,帮助企业选择一个最佳方案使所获利润最多? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为正三角形ABC内一点,PA=2,PB=4,PC=2
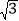 ,则正三角形ABC的面积为_____.
,则正三角形ABC的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一张厚度是0.2毫米的纸,如果将它连续对折10次,那么它会有多厚?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察如图所示的图形,并阅读相关文字信息后回答下列问题:
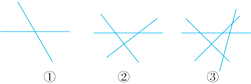
2条直线相交,最多有1个交点;3条直线相交,最多有3个交点;4条直线相交,最多有6个交点.
(1)8条直线相交,最多有几个交点?
(2)设有n条直线相交,最多有y个交点,请用含n的代数式表示y.
(3)当最多交点个数为4950时,此时直线有几条?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,AB=CD,请添加一个条件_____,使得四边形ABCD是平行四边形.
相关试题

